Question 901776: Good day
I have something puzzling me for quite a while now
Let't take an example
In the quadratic equation
1. 72c2 + 24c - 16
The answer is (12c - 4) (6c + 4)
Firstly.. Why 12 and 6? why not something like 9 and 8
Tried the formula with this example numbered as "1."
Secondly.. How do I know from the equation "72c2 + 24c - 16" which bracket is going to get the "+" and which bracket is going to get the "-"
They explained it in school but I just can't remember the principles.
Kind Regards.
Stefan.
Found 4 solutions by ewatrrr, MathTherapy, Alan3354, richwmiller:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! 72c^2 +  - 16 = (12c - 4)(6c+4) - 16 = (12c - 4)(6c+4)
Why? Check with FOIL
F First terms 72c^2
O Outside terms 48c
I Inside terms -24c Note(48c-24c =  ) )
L Last terms -16
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Good day
I have something puzzling me for quite a while now
Let't take an example
In the quadratic equation
1. 72c2 + 24c - 16
The answer is (12c - 4) (6c + 4)
Firstly.. Why 12 and 6? why not something like 9 and 8
Tried the formula with this example numbered as "1."
Secondly.. How do I know from the equation "72c2 + 24c - 16" which bracket is going to get the "+" and which bracket is going to get the "-"
They explained it in school but I just can't remember the principles.
Kind Regards.
Stefan.

The first thing, when factoring this trinomial is to factor out the GCF, which is 8.
Thus,  becomes: becomes:  , after which, , after which,  should be factored. should be factored.
Final factors: 
It's confusing when c is the variable in the trinomial, so it's better to
change  to to  ....same thing, just that the variable was changed from c to x. ....same thing, just that the variable was changed from c to x.
Without factoring out a GCF, and applying the "ac" method, we would need two factors with a product
of - 1,152 (a * c, or 72 * - 16), and that SUM to "b" (+ 24). These factors are: + 48 and - 24.
We now replace + 24x in the trinomial,  with + 48x - 24x. I hope you're following!! with + 48x - 24x. I hope you're following!!
Now,  becomes: becomes:  . At this point, I'd switch the variable, x back to c, . At this point, I'd switch the variable, x back to c,
so we now have: 
The factors are now obtained by grouping the first two binomials, and then the last two binomials, so that results in:
 , and the final answer: , and the final answer:  , which is the same as your factors: , which is the same as your factors:  . .
Factoring these further, results in:  , the CORRECT factors. , the CORRECT factors.
However,  and and  are incorrect as the GCF of the original polynomial should be obtained are incorrect as the GCF of the original polynomial should be obtained
and factored out first. I only went this far to explain the procedure to determine the correct factors when
leading-coefficient multiples such as 24, 36, 72, and others are part of polynomials that need to be factored.
These and other leading-coefficient multiples pose a problem at times since they have as many as 4 or 5 sets of
factors, and can be pretty tedious to factor correctly.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! In the quadratic equation
1. 72c2 + 24c - 16
---------------
That's not an equation, there's no equal sign.
The answer is (12c - 4) (6c + 4)
------------
I would say it's 8*(3c-1)*(3c+2)
-------
The short answer is, because 9 and 8 don't work. If you factor out the 8 first, it's obvious it can't be 9 and 8.

Then you might ask, "Why 3 and 3, and not 9 and 1?"
You can't get the middle term to be 3c using 9 and 1.
-------
Factor out any coefficients first, it'll make it simpler.
Use ^ (Shift 6) for exponents.
eg, c^2
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website!
| Solved by pluggable solver: Factoring using the AC method (Factor by Grouping) |
 Start with the given expression. Start with the given expression.
 Factor out the GCF Factor out the GCF  . .
Now let's try to factor the inner expression 
---------------------------------------------------------------
Looking at the expression  , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is  , and the last term is , and the last term is  . .
Now multiply the first coefficient  by the last term by the last term  to get to get  . .
Now the question is: what two whole numbers multiply to 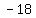 (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient  ? ?
To find these two numbers, we need to list all of the factors of 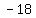 (the previous product). (the previous product).
Factors of 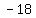 : :
1,2,3,6,9,18
-1,-2,-3,-6,-9,-18
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to 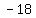 . .
1*(-18) = -18
2*(-9) = -18
3*(-6) = -18
(-1)*(18) = -18
(-2)*(9) = -18
(-3)*(6) = -18
Now let's add up each pair of factors to see if one pair adds to the middle coefficient  : :
| First Number | Second Number | Sum | | 1 | -18 | 1+(-18)=-17 | | 2 | -9 | 2+(-9)=-7 | | 3 | -6 | 3+(-6)=-3 | | -1 | 18 | -1+18=17 | | -2 | 9 | -2+9=7 | | -3 | 6 | -3+6=3 |
From the table, we can see that the two numbers  and and  add to add to  (the middle coefficient). (the middle coefficient).
So the two numbers  and and  both multiply to both multiply to 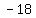 and add to and add to 
Now replace the middle term 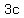 with with  . Remember, . Remember,  and and  add to add to  . So this shows us that . So this shows us that  . .
 Replace the second term Replace the second term 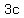 with with  . .
 Group the terms into two pairs. Group the terms into two pairs.
 Factor out the GCF Factor out the GCF 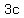 from the first group. from the first group.
 Factor out Factor out  from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis. from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis.
 Combine like terms. Or factor out the common term Combine like terms. Or factor out the common term 
--------------------------------------------------
So  then factors further to then factors further to 
===============================================================
Answer:
So  completely factors to completely factors to  . .
In other words,  . .
Note: you can check the answer by expanding  to get to get  or by graphing the original expression and the answer (the two graphs should be identical). or by graphing the original expression and the answer (the two graphs should be identical).
|
|
|
|