Question 89451: Please help me on how to figure out the vertex of the equation 2y=x2(this is x squared)-2x-5.
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help me on how to figure out the vertex of the equation 2y=x2(this is x squared)-2x-5.
----------------
2y=x^2-2x-5
Complete the square on the x-terms and keep the equation balanced:
2y+5+1 = x^2-2x+1
2(y+3) = (x-1)^2
-----------
The vertex is at (1,-3)
-----------------------
Another way to find it:
y = (1/2)x^2-x-(5/2)
The vertex occus when x=(-b)/(2a) = 1/(2*(1/2)) = 1/1=1
Solve for y to get the y coordinate:
y = (1/2)1^2-1-(5/2) = (1/2)-1(-5/2) = -6/2 = -3
===============
Cheers,
Stan H.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
2y = x² - 2x - 5
Method 1:
Get it in the form
y = a(x - h)² + k
where the vertex is (h,k) and the two neighbor
points are (h±1,k+a)
Take one-half of the coefficient of x, which is
one-half of -2 or -1. Then square -1 and get
+1 then add +1 to both sides
2y + 1 = x² - 2x + 1 - 5
Factor the first three terms on the right
2y + 1 = (x - 1)(x - 1) - 5
Write (x - 1)(x - 1) as (x - 1)²
2y + 1 = (x - 1)² - 5
Add -1 to both sides:
2y = (x - 1)x² - 6
Divide every term by 2:
y =  (x - 1)² - 3
Compare to the standard equation:
y = a(x - h)² + k
and we see that a = (x - 1)² - 3
Compare to the standard equation:
y = a(x - h)² + k
and we see that a =  , h = 1, k= -3
So the vertex is
(h,k) = (1,-3)
That's all you wanted but you should take
this opportunity to learn to graph.
The two neighbor points
are (h±1,k+a) = (1±1, -3+ , h = 1, k= -3
So the vertex is
(h,k) = (1,-3)
That's all you wanted but you should take
this opportunity to learn to graph.
The two neighbor points
are (h±1,k+a) = (1±1, -3+ ) which are
(0, ) which are
(0, ) and (2, ) and (2, )
We can draw the graph by plotting those three
points first )
We can draw the graph by plotting those three
points first
 Then sketch a parabola through those three
points:
Then sketch a parabola through those three
points:
 Another way just to find the vertex is to
memorize the vertex formula:
----------------------
The general equation y = ax² + bx + c
has vertex (h,k) where
h =
Another way just to find the vertex is to
memorize the vertex formula:
----------------------
The general equation y = ax² + bx + c
has vertex (h,k) where
h =  k = the value of y when h is substituted for x
-----------------------
So for
2y = x² - 2x - 5
Get it in general form y = ax² + bx + c
Divide through every term by 2
y =
k = the value of y when h is substituted for x
-----------------------
So for
2y = x² - 2x - 5
Get it in general form y = ax² + bx + c
Divide through every term by 2
y = 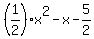 Compare to the general form
y = ax² + bx + c
and we see that
a =
Compare to the general form
y = ax² + bx + c
and we see that
a =  , b = -1, c = , b = -1, c =  h =
h =  = = 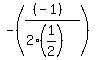 = = 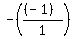 = = 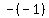 = 1
k = the value of y when 1 is substituted for x
y = = 1
k = the value of y when 1 is substituted for x
y = 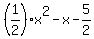 y =
y = 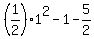 = = 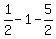 = = 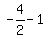 = = 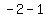 = =  So k = -3
So the vertex by this method is also (h,k) = (1,-3)
Edwin
So k = -3
So the vertex by this method is also (h,k) = (1,-3)
Edwin
|
|
|