Question 890611: If i have roots or solution m and n, what can i do to identify the standard form of the given roots?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! IN GENERAL:
A quadratic equation is an equation of degree  , so you know that there will be an , so you know that there will be an  somewhere. somewhere.
If you know that  and and  are solutions (or roots) of a quadratic equation, are solutions (or roots) of a quadratic equation,
you can write a quadratic equation with those solutions as
 . .
That is the equation in factored form.
If you multiply the factors  and and  and simplify the result, and simplify the result,
you get a more elegant quadratic equation that your teacher will like better.
There are infinite quadratic equations with those roots (or solutions).
You can transform a quadratic equation into an equivalent one
(one with exactly the same solutions, no more or less solutions, no different solutions)
by multiplying both sides of the equation by a number other than zero:
Take any 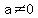 , and , and
 ---> --->  ---> ---> 
(If you multiplied both sides times zero you would end up with  that is not much of an equation). that is not much of an equation).
EXAMPLE:
For example, if the solutions or roots of a quadratic equation are  and and  , I would write , I would write
 ---> --->  ---> --->  ---> --->  ---> --->  ---> ---> 
All those equations are equivalent, but the last one is the simplest and most elegant of them.
I could multiply both sides times a non-zero number, let's say  , to get an elegant but unnecessarily complicated equation: , to get an elegant but unnecessarily complicated equation:
 . .
EXTRA:
Also, with the same roots I can write equations of a degree higher than  (not quadratic), (not quadratic),
by multiplying both sides times some polynomial, like  or or 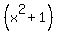 . .
|
|
|