Question 874959: pleae answe these qustion
1.find two numbers whose sum is 13 and whose product is 40
2.the area of a rectangle is 94sq. units and its perimeter is 38units.
find the length and width of the rectangle.
thanks
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. You can set up a quadratic equation and solve it, and that may be what is expected, but it is not the most efficient way.
THE FIFTH GRADER WAY:
The most effective way would be to find pairs of factors whose product is 
and see if the sum of one of those pairs is  : :
 and and  so it is not so it is not 
 and and  so it is not so it is not 
 and and  so it is not so it is not 
 and and  so the answer is so the answer is  and and  . .
I did not even need to mention "quadratic equations" or know what the term means.
INVOKING QUADRATIC EQUATIONS:
 = one of the numbers = one of the numbers
 = the other number = the other number
Since we know they add to  , ,
 ---> --->
So the product of the two numbers is



I see 3 ways to solve that quadratic equation.
1) I would factor it into 
and then make each factor equal to zero.
Factoring really means doing the work the fifth grader would do,
and I believe that is the most efficient way to solve this particular quadratic equation.
 ---> ---> --> --> ---> --->
 ---> ---> --> --> ---> --->
Either solution tells us that the two numbers are  and and  . .
2) we could use the quadratic formula that says that the solutions to
 are given by are given by

For  , ,  , ,  , and , and  , so , so

That gives us the answers
 ---> ---> ---> ---> and and
 ---> ---> ---> ---> as above. as above.
3) The third option is completing the square:







So either  ---> ---> ---> ---> ---> ---> or or
 ---> ---> ---> ---> ---> ---> . .
Any way you solve the quadratic equation, the two numbers are  and and  . .
2. You have to find two numbers that are the measurements of  and and 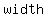 for that rectangle. for that rectangle.

so 

so 


THE FIFTH GRADER WAY/WITHOUT MENTIONING QUADRATIC EQUATIONS:
Could it be a square?
If it was a square with a side length of  units, units,
The perimeter would be  ---> ---> --> --> units units
The area of that square would be  square units . square units .
A square with a perimeter of  units has an area of units has an area of  square units, and we are asked to find a larger rectangle with the same perimeter and an area of square units, and we are asked to find a larger rectangle with the same perimeter and an area of 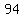 square units . square units .
There is something wrong with this problem.
In the real world there is no such a rectangle.
Maybe there was a typo, or maybe it is a trick question,
because we know, from all those fencing-a-square-pen problems, that the largest rectangle we can make with a given perimeter is a square.
There are no real length and width measurements for that rectangle.
Could it be that the measurements are imaginary numbers?
The fifth grader goes to the computer to do a search on "imaginary numbers."
THE QUADRATIC WAY:
So the sum of those two measures is  and the product is and the product is 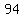 . .
This problem is similar to the one above, but factoring does not always work.
Sometimes factoring is complicated,
Sometimes the solutions are irrational numbers, so you would have to write a quadratic equation and try to solve it by using the quadratic formula or completing the square.
Sometimes there are no real solutions.
In all those cases, the quadratic formula (or completing the square) would tell us the answer.
If one of those measures is  , the other will be , the other will be 
and  --> -->  --> -->
To apply the quadratic formula,
 , ,
for this equation  , ,  , and , and  . .
Applying the quadratic formula,



We have no real solutions, because  is no real number, is no real number,
so there are no real solutions, but we could ask that fifth grader about imaginary ones.
|
|
|