SOLUTION: solve the equation by completeing the square a2(squared)-12a+27=0

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: solve the equation by completeing the square a2(squared)-12a+27=0      Log On


   

Question 86802: solve the equation by completeing the square
a2(squared)-12a+27=0
Found 2 solutions by stanbon, jim_thompson5910:
Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
solve the equation by completing the square
a^2-12a+27=0
-----------
a^2-12a+? = -27+?
Complete the square.
a^2-12a+(12/2)^2 = -27 + (12/2)^2
(a-6)^2 = -27 + 36
(a-6)^2 = 9
(a-6) = 3 or (a-6) = -3
a = 9 or a = 3
=======================
Cheers,
Stan H.

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
note: I'm going to use "x" instead of "a" as my variable
We can convert any quadratic ax%5E2%2Bbx%2Bc to standard vertex form 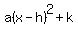a%28x-h%29%5E2%2Bk by this procedure:
y=%281%29%2Ax%5E2-%2812%29%2Ax%2B27 Start with the given quadratic


y-27=%281%29%2Ax%5E2-%2812%29%2Ax Subtract 27 from both sides

y-27=%281%29%2A%28x%5E2-%2812%29%2Ax%29 Factor out the leading coefficient1
Now to complete the square on the right side we must take half of the x coefficient (in ax%5E2%2Bbx%2Bc its b) and square it (i.e. %28b%2F2%29%5E2)

y-27=%281%29%2A%28x%5E2-%2812%29%2Ax%2B36%29 Take half of -12 and square it (ie %28%28-12%29%281%2F2%29%29%5E2). Add the result(36) just inside the parenthesis.


This completes the square on the right side. So it goes from%281%29%2A%28x%5E2-%2812%29%2Ax%2B36%29 and factors to %281%29%2A%28x-6%29%5E2 which is a perfect square

y-27=%281%29%2A%28x-6%29%5E2 Factor the right side into a perfect square
Since we added 36 inside the parenthesis, we really added %281%29%2836%29 to the entire right side (just distribute the leading coefficient 1 and you'll see it). So we must add %281%29%2836%29 to the other side to balance the equation.

y-27%2B%281%29%2A%2836%29=%281%29%2A%28x-6%29%5E2 Add %281%29%2836%29 to the other side


y-27%2B36=%281%29%2A%28x-6%29%5E2 Multiply
y-27%2B36=%281%29%2A%28x-6%29%5E2 Reduce

y%2B9=%281%29%2A%28x-6%29%5E2 Combine like terms on the left side

y%2B9=%281%29%2A%28x-6%29%5E2 Reduce any fractions left side
y=%281%29%28x-6%29%5E2-9Subtract 9 from both sides
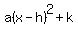So the quadratic y=%281%29%2Ax%5E2-%2812%29%2Ax%2B27 is completed to y=%281%29%2A%28x-6%29%5E2-9 which is now in vertex form (which is a%28x-h%29%5E2%2Bk) where a=1 (the stretch/compression factor), h=6(the x-coordinate of the vertex), and k=-9 is the y coordinate of the vertex. So this means the vertex is (6,-9). Also, since the axis of symmetry is the vertical line through the vertex, the axis of symmetry is x=6 (it is equal to the x-coordinate of the vertex).
Here are the graphs of original quadratic y=%281%29%2Ax%5E2-%2812%29%2Ax%2B27 and our answer in vertex form y=%281%29%28x-6%29%5E2-9
graph of y=%281%29%2Ax%5E2-%2812%29%2Ax%2B27 with the vertex (6,-9) and the axis of symmetry x=6 (it is the vertical line through the vertex)

graph of y=%281%29%28x-6%29%5E2-9 with the vertex (6,-9) and the axis of symmetry x=6 (it is the vertical line through the vertex)

Notice the two graphs are equivalent; this verifies our answer.

Now to solve for x, we simply need to isolate x:
0=%281%29%2A%28x-6%29%5E2-9 Set y equal to zero to solve for x
0%2B9=%281%29%2A%28x-6%29%5E2Add 9 to both sides
0%2B-sqrt%289%29=x-6 Take the square root of both sides
Take the square root
Add 6 to both sides

So it breaks down to this
x=6-3 or x=6%2B3

So our solution is

x=3 or x=9


Notice if you look back at the graph, you will see the roots x=3 and x=9. This verifies our answer