Question 788874: A producer of synfuel from coal estimates that the cost C dollars per barrel for a production run of x thousand barrels is given by C = 9x^2 - 180x + 940. How many thousand barrels should be produced each run to keep the cost per barrel at a minimum? What is the minimum cost per barrel of synfuel?
Can you please help me out? Thanks so much in advance:)
Can you also please show the steps it would really help me understand:) Thank-you
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  describes C as a quadratic function of x.
The graph (with C as the y coordinate) is 
That curve is called a parabola, and the pointy end is called the vertex of the parabola.
In this case it is a minimum value for C and it happens when x=10, and C=40.
There is more than one way to find the coordinates (x and C) for that minimum point in the graph.
You can apply formulas (memorized or copied, understood, or not).
Another option is to "complete the square" transforming the equation into a form that will give away its secrets.
WITH FORMULAS:
A function of the form  or  , with 
is called a quadratic functiuon, and graphs as a parabola.
Its axis of symmetry and vertex are at  .
If you find that value of the x-coordinate at the vertex, you can substitute it into the function to find the y-coordinate.
Otherwise you can apply another, more complicated formula to find the y-coordinate at the vertex.
The vertex will be a maximum of the function if 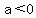 , and it will be a minimum if  .
In this case,  , so we have a minimum, and  .
So, at the minimum 
Plugging that value into we find the minimum value for C:
COMPLETING THE SQUARE:
That last form of the equation tells you that there is a minimum, that the minimum will happens when  and  , and that the curve is very pointy, getting 9 times taller that it is wide for x one unit away from its center, and rising very sharply to the left and right.
|
|
|
