Question 7426: 5x^2 + bx + 1 = 0
I am supposed to find all values of b that give one or more real number solutions. Please help me. I could'nt come up with anything.
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! I would use the discriminant trick here. It's the formula 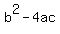 . The variables a, b, and c can be obtained from a quadratic equation in standard form, like the one you've got. . The variables a, b, and c can be obtained from a quadratic equation in standard form, like the one you've got.
The discriminant's value ONLY tells you WHETHER the quadratic value has 0,1, or two solutions. Whatever its value is, how high or low it is has nothing to do with the actual solution! The rule is, if you want one or more solutions, you want that discriminant's value to be greater than or equal to zero, and it doesn't matter what the discriminant's value is AS LONG AS it turns out greater than or equal to zero.
You've got a = 5 and c = 1. But you don't have b. That's the one we're to find. So, we'll set it up this way: 
You've got a and c, so let's plug those in:  which really is which really is  . That's a difference of squares look-alike, but the 20 is not a perfect square. It's all good. That's equal to . That's a difference of squares look-alike, but the 20 is not a perfect square. It's all good. That's equal to  . <---- If you performed FOIL on this, you'll get back to your original expression. It's alright to do this. . <---- If you performed FOIL on this, you'll get back to your original expression. It's alright to do this.
If that were an equals sign, your answer would already be  and and  . But since it's an inequality, your answer will be in intervals. The . But since it's an inequality, your answer will be in intervals. The  and and  are just your critical points, serving as boundaries to your intervals. Actually these two critical points divide your number line into 3 intervals - (-infinity, are just your critical points, serving as boundaries to your intervals. Actually these two critical points divide your number line into 3 intervals - (-infinity, ], ],
( , , ), and [ ), and [ ,infinity). ,infinity).
What you would do now is to test values that fall within each of these three ranges. For the (-infinity, ], let's choose -10 and plug it into the inequality we had: ], let's choose -10 and plug it into the inequality we had:  is right. Just be cause the -10 worked and is within the interval, so will all the values in that interval. So far, b can be ANYTHING as long as it's less than square root of 20. is right. Just be cause the -10 worked and is within the interval, so will all the values in that interval. So far, b can be ANYTHING as long as it's less than square root of 20.
What about that middle interval between  and and  ? Let's pick the value 0 because it's easy and it falls within the range. You'll get ? Let's pick the value 0 because it's easy and it falls within the range. You'll get  which is false. That 0 value didn't work, so all the values within the range won't work also. which is false. That 0 value didn't work, so all the values within the range won't work also.
If you choose to plug in a number greater than  though, you'll get a positive value for the discriminant. Say we choose 11: though, you'll get a positive value for the discriminant. Say we choose 11:  is clearly true. Since 11 works, so will any number greater than or equal to is clearly true. Since 11 works, so will any number greater than or equal to  . .
So, the possible values for b in this case will be anything less than 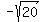 and anything greater than and anything greater than  . .
|
|
|