SOLUTION: Two pipes can fill up water tank in 6 hours and 40 minutes. Find the time each will take to fill the tank if one of the two pipes can fill it is three hours less than the other.

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: Two pipes can fill up water tank in 6 hours and 40 minutes. Find the time each will take to fill the tank if one of the two pipes can fill it is three hours less than the other.      Log On


   

Question 726700: Two pipes can fill up water tank in 6 hours and 40 minutes. Find the time each will take to fill the tank if one of the two pipes can fill it is three hours less than the other.
Found 2 solutions by checkley79, Edwin McCravy:
Answer by checkley79(3341) About Me  (Show Source):
You can put this solution on YOUR website!
1/X+1/(X-3)=1/6.67
(X-3+X)/X(X-3)=1/6.67
(2X-3)/(X^2-3X)=1/6.67 CROSS MULTIPLY.
6.67(2X-3)=X^2-3X
13.33X-20=X^2-3X
X^2-3X-13.33X+20=0
X^2-16.33X+20=0
(X-15)(X-1.33)=0
X-15=0
X=15 HOURS.
15-3=12 HOURS.
PROOF:
1/15+/1/12=1/6.67
(15+12)/15*12=1/6.67
27/180=1/6.67
180=27*6.67
180=180

Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
Here it is with explanation and also without rounded-off decimals.

Two pipes can fill up a water tank in 6 hours and 40 minutes. 
"6 hours and 40 minutes" is 6%2640%2F60 hours or 6%262%2F3 hours. 

Their combined tank-filling rate is 1 tank per 6%262%2F3 hours, or

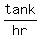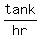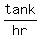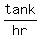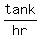
1_tank%2F6%262%2F3hr = 1%2F%286%262%2F3%29tank%2Fhr = 1%22%F7%226%262%2F3tank%2Fhr = 1%22%F7%2220%2F3tank%2Fhr = 1%2A3%2F20tank%2Fhr = 3%2F20tank%2Fhr

Find the time each will take to fill the tank 
Let x = the number of hours it takes the slower pipe to fill the tank
alone.

The slower pipe's tank-filling rate is 1 tank per x hours, or

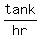
1_tank%2F%28x_hr%29 = 1%2Fxtank%2Fhr

if one of the two pipes can fill it is three hours less than the other.
Then x-3 = the number of houts it takes the faster pie to fill the tank alone.

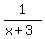
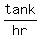The faster pipe's tank-filling rate is 1 tank per x-3 hours, or 1_tank%2F%28x%2B3_hr%29 = 1%2F%28x%2B3%29tank%2Fhr

The equation comes from

          %28matrix%285%2C1%2C%0D%0ASLOWER%2C%22PIPE%27S%22%2CTANK%2CFILLING%2CRATE%29%29%22%22%2B%22%22%28matrix%285%2C1%2C%0D%0AFASTER%2C%22PIPE%27S%22%2CTANK%2CFILLING%2CRATE%29%29%22%22=%22%22%28matrix%285%2C1%2C%0D%0ATHEIR%2CCOMBINED%2CTANK%2CFILLING%2CRATE%29%29

                    1%2Fx%22%22%2B%22%22%7D%7B%7D%7D%7B%7B%7B1%2F%28x-3%29%22%22=%22%223%2F20

Multiply through by 20x(x-3)

                    20(x-3) + 20x = 3x(x-3)
                     20x-60 + 20x = 3x²-9x
                           40x-60 = 3x²-9x
                                0 = 3x²-49x+60
                                0 = (x-15)(3x-4)

                                    x-15 =  0;   3x-4 = 0
                                       x = 15;     3x = 4
                                                    x = 4%2F3
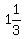                                                    x = 1%261%2F3

We discard the x = 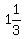1%261%2F3 because the slower's rate cannot be faster 
that the combined rate.

Answer:  The slower one takes 15 hours and the faster one 3 hours less,
or 12 hours.

Edwin