Question 720500: if you drop an object off the roof of an apartment building that is 240 feet tall, about how long will it take the object to hit the ground?
Found 2 solutions by jsmallt9, Alan3354:
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! A general equation for this type of problem is:

where...- "t" is a number of units of time that have passed since some starting point in time. (Often, the units are seconds.)
- "s" is a position/distance/height after t units of time.
- "g" is the acceleration due to gravity. If we're on Earth and we're measuring distances in feet then this number is 32. (If we're on Earth and we're measuring distances in meters then this number is 9.8. )
 is the initial velocity/speed. (IOW, the velocity at t = 0) is the initial velocity/speed. (IOW, the velocity at t = 0)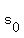 is the initial position/distance/height. (IOW, the position at t = 0) is the initial position/distance/height. (IOW, the position at t = 0)
In this problem,
g = 32 (since our distances are measured in feet)
 (since we're just dropping the object, not throwing it) (since we're just dropping the object, not throwing it)
 (since the object starts 240 feet above the ground) (since the object starts 240 feet above the ground)
So the equation for this problem is:

which simplifies to:

Since the ground is where the height is zero, the solution to "how long will it take to get to the ground" will be found by replacing the s with 0 and solving for t:

Factoring out -16:

(Notice how factoring out -16 results in the other factor,  being easier to factor than if we had factored out 16, being easier to factor than if we had factored out 16,  ). Factoring the difference of squares: ). Factoring the difference of squares:

From the Zero Product Property:
-16 = 0 or t+3 = 0 or t-3 = 0
The first equation is a false statement. We will get no solutions from that equation. But we can solve the other two:
t = -3 or t = 3
Since t is the number of seconds since the object was dropped, a negative time makes no sense. t = -3 means "the object will hit the ground 3 seconds before we dropped it!?" So we reject this solution. Therefore the only solution is t = 3, or "the object hits the ground 3 seconds after we dropped it."
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you drop an object off the roof of an apartment building that is 240 feet tall, about how long will it take the object to hit the ground?
-----------------
s = 16t^2 is commonly used for acceleration on Earth due to gravity (in feet)
240 = 16t^2
t^2 = 15
t = sqrt(15) seconds
=~ 3.873 seconds
|
|
|