Question 660402: a rectangular pasture is to be fenced along 4 sides and divided into three parts by two fences parallel to one of the sides. find the dimensions of the pasture if the total amount of fencing is 800 yards and the area of the pasture is 9200 yards square . . algebra.com
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! A rectangular enclosure, fenced along 4 sides, and divided into three parts by two fences parallel to one of the sides, would look like this:
If the length of each of the four parallel fence sections is  yards,
and the length of the other sections of fencing is  yards,
the area, 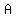 , of the whole enclosure, in square yards, is
 , which is supposed to equal 9200 yards.
The total length of the fencing, in yards, is
 -->  --> 
Substituting that expression for , the area of the enclosure, in square yards, is
 -->  , which is supposed to equal 9200 yards.
That gives us the quadratic equation  .
With a little algebra, we can rearrange it into a standard form:
-->  ,
and dividing everything by  we get
 , which I like even better.
Using the quadratic formula, 
we solve that equation.
 = about  (rounding)
So a good approximation of the two solutions would be
One solution is  -->  -->  ,
which substituted into
gives  -->  --> 
The other solution is  -->  -->  ,
which substituted into
gives  -->  --> 
|
|
|
