Question 609154: Y=2x(squared)-8x-1
i wanna know the a vaule b vaule and c vaule i also wanna know if it opens up or down? the axis of symmetry the vertex the domain and the range
Found 2 solutions by ewatrrr, Edwin McCravy:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Using the vertex form of a parabola,  where(h,k) is the vertex where(h,k) is the vertex
y = 2x^2 - 8x - 1 ||Note the use of ^(uppercase 6) to signify the exponent
y = 2(x-2)^2 - 8 - 1 || completing the Square
y = 2(x-2)^2 - 9 || V(2,-9)min, a = 2>0, Parabola opens Upward, Range is y≥ -9, domain x is (−∞,∞)

Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I do it the "vertex formula" way
y = 2x² - 8x - 1
Compare your equation to this model:
y = ax² + bx + c
It's easy to see that a=2, b=-8, c = -1
We know that it opens upward because "a" is a positive number.
The vertex formula is:
The vertex or turning point is (h,k) where h =  and
k = ah²+bh+c and the axis of symmetry is the vertical line whose
equation is x = h
So for your vertex, h = and
k = ah²+bh+c and the axis of symmetry is the vertical line whose
equation is x = h
So for your vertex, h = 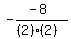 = = 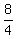 = 2
and k = ah²+bh+c = (2)(2)²+(-8)(2)+(-1) = 2(4)-16-1 = 8-16-1 = -9
So the vertex is (h,k) = (2,-9)
The y-intercept is found by letting x=0 in the original equation:
y = 2x² - 8x - 1
y = 2(0)² - 8(0) - 1
y = -1
The y-intercept is the point (0,-1)
So we plot the vertex the axis of symmetry and the y-intercept: = 2
and k = ah²+bh+c = (2)(2)²+(-8)(2)+(-1) = 2(4)-16-1 = 8-16-1 = -9
So the vertex is (h,k) = (2,-9)
The y-intercept is found by letting x=0 in the original equation:
y = 2x² - 8x - 1
y = 2(0)² - 8(0) - 1
y = -1
The y-intercept is the point (0,-1)
So we plot the vertex the axis of symmetry and the y-intercept:
 Now you can draw in the parabola so that it is symmetrical with
the green line of symmetry.
Now you can draw in the parabola so that it is symmetrical with
the green line of symmetry.
 All x-values are in the domain, so the domain is all reals (
All x-values are in the domain, so the domain is all reals ( , ,  )
The only y-values are those from the vertex which is -9 upward,
so the range is (-9, )
The only y-values are those from the vertex which is -9 upward,
so the range is (-9, ).
Edwin ).
Edwin
|
|
|