Question 560290: 64k^2+112k+49=0 I've tried several times to solve this equation. Would you please solve it and I'll practice others. Thank you!!
Found 2 solutions by stanbon, bucky:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! 64k^2+112k+49=0
---
sqrt(64k^2) = 8k
sqrt(49) = 7
----
2*7*8k = 112k
-------
So the expression is the square of a binomial.
--
Ans: (8k+7)^2
==========================
Cheers,
Stan H.
Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website! Given to solve:
.
.
This equation is in the standard quadratic equation form of:
.
.
and by comparing terms, we can see that a (the multiplier of the k-squared term) is +64, b (the multiplier of the k term) is +112, and c (the constant) is +49.
.
The quadratic formula says that if you have an equation of the standard quadratic form, the answer for k is given by:
.
.
For this problem, we identified the values for a as +64, b as +112, and c as +49. So we substitute those values into the equation for k to get:
.
.
Inside the radical sign the 112 squared equals 12544 and the -4*64*49 equals -12544. Then in the denominator 2 * 64 = 128. When these values are substituted into the equation for k, the equation becomes:
.
.
Notice that the terms inside the radical result in it becoming zero. So the equation for k is reduced to:
.
.
Since the numerator and denominator are both even numbers, they are both divisible by some power of 2. For openers, let's try reducing them by dividing both by 8 to get:
.
.
and both the numerator and denominator are again even numbers. Dividing them both by 2 gives the answer:
.
.
You can check this answer by returning to the equation that was given originally in the problem:
.
.
and substituting  for k as follows:
.
.
squaring results in 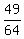 and substituting this gives:
.
.
Cancel the 64 in the numerator and denominator:
.
.
This reduces the equation to:
.
.
Add the two terms of 49 and the equation becomes:
.
.
Notice in the second term the denominator 8 divides exactly into 112 to give 14. So the equation reduces to:
.
.
and 14 times -7 is -98 which makes the equation:
.
.
This is obviously true, so the answer of checks and is, therefore, a correct answer.
.
I hope this helps you over the rough spot where you encountered difficulty with this problem.
.
|
|
|
