Question 541963: The question from my book says that "the radicand of the quadratic formula, b^2 - 4ac, can be used to determine whether  has solutions that are rational, irrational, or not real numbers." I haven't been able to solve the problem on this website because it's saying that the first coefficient is zero. It's also asking me to explain how this works. And if it possible to determine the kinds of answers that one will obtain to a quadratic equation without actually solving the equation. I would greatly appreciate any help I can get. has solutions that are rational, irrational, or not real numbers." I haven't been able to solve the problem on this website because it's saying that the first coefficient is zero. It's also asking me to explain how this works. And if it possible to determine the kinds of answers that one will obtain to a quadratic equation without actually solving the equation. I would greatly appreciate any help I can get.
Found 2 solutions by neatmath, josmiceli:
Answer by neatmath(302)   (Show Source): (Show Source):
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! The quadratic formula is:

I will make the replacement

Now I have

and

------------------
If  is not zero and is a real number, I is not zero and is a real number, I
get a different solution for each equation,
so 2 solutions.
-------------
If  , then there is only 1 solution , then there is only 1 solution
-------------
Also, since  is a square root, it can be is a square root, it can be
 , which is , which is 
and there are 2 imaginary solutions.
-------------------------------
These possibilities depend on what
 is is
 = 0 ( one solution ) = 0 ( one solution )
 = (+) ( two real solutions ) = (+) ( two real solutions )
 = (-) ( two imaginary solutions ) = (-) ( two imaginary solutions )
------------------
In the case of  = (+), if this is a perfect square, = (+), if this is a perfect square,
like  The 2 real solutions will be rational, which means The 2 real solutions will be rational, which means
a fraction of some kind.
If it is not a perfect square, like 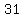 , the 2 real solutions , the 2 real solutions
will be irrational, like  . . . forever . . . forever
-------------------
Hope this isn't confusing.
|
|
|