Question 472862: I have to find the x and y intercepts axis of symmentary and vertex of this equation
y= -x^2/2+3x+8
to find x intercepts told to mutiply by -2, which makes equation
y=x^-6x-16
would I find axis of symmentry and vertex from the new values or from original equation.
Found 2 solutions by ewatrrr, MathLover1:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
y= -x^2/2+3x+8
0 = -x^2/2+3x+8 | x-intercepts when y = 0
0 = x^2 - 6x -16 = (x-8)(x+2) x-intercepts (8,0)(-2,0)
the vertex form of a parabola,  where(h,k) is the vertex where(h,k) is the vertex
y= -x^2/2+3x+8 |complete the square of the original EQ
y= -(1/2)[ x-3)^2 -9] + 8
y= -(1/2)[ x-3)^2 + 25/2 V(3,12.5)

Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! The  occurs when occurs when  , make the equation = , make the equation =  and solve for and solve for 

 ......... multiply by ......... multiply by 
 .......or .......or
 .........use quadratic formula .........use quadratic formula





solutions:



or



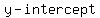 occurs when occurs when  , substitute , substitute  for for  in the equation, and find in the equation, and find 



so, the  are at points ( are at points ( , , ) and ( ) and ( , , ) )
the 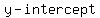 is at point ( is at point (  ) )
Axis of symmetry can be found using the formula: 
since  and and  , ,

so, the axis of symmetry is 
Vertex is the x/y values for the max or min and occurs at the axis of symmetry; so Substitute  for for  and find the and find the  value: value:




so, the Vertex is at ( , ,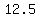 ) )
now see it on a graph:

|
|
|