Question 408299: Given one roots of x^2+px+8=0 is two times of the other. Find the roots and p.
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Interesting thing about this problem is that the roots and the value of p are not uniquely determined. You'll see why:
Suppose the two roots are  and and  . The product of the roots is 8 by Vieta's formulas, so . The product of the roots is 8 by Vieta's formulas, so  --> -->  --> r = +/- 2. Hence, the roots are {2, 4} or {-2, -4}. Also, the sum of the roots is -p, so p = -6 or 6, respectively. --> r = +/- 2. Hence, the roots are {2, 4} or {-2, -4}. Also, the sum of the roots is -p, so p = -6 or 6, respectively.
Hence, the quadratic  has roots {2, 4} and has roots {2, 4} and 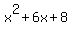 has roots {-2, -4}. has roots {-2, -4}.
|
|
|