SOLUTION: what is the vertex of a parabola that is pointing downward and contains the points (-2,2), (0,1), and (1,2.5).

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: what is the vertex of a parabola that is pointing downward and contains the points (-2,2), (0,1), and (1,2.5).       Log On


   

Question 336452: what is the vertex of a parabola that is pointing downward and contains the points (-2,2), (0,1), and (1,2.5).
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
The general equation for a parabola is y=ax%5E2%2Bbx%2Bc
Solve for a,b, and c using the points (-2,2), (0,1), and (1,2.5).
+2=a%28-2%29%5E2%2Bb%28-2%29%2Bc
+4a-2b%2Bc=2
.
.
.
+1=a%280%29%5E2%2Bb%280%29%2Bc
+highlight_green%28c=1%29
.
.
.
+5%2F2=a%281%29%5E2%2Bb%281%29%2Bc
+a%2Bb%2Bc=5%2F2
Simplify with c=1
4a-2b%2B1=2
1.4a-2b=1
.
.
.
a%2Bb%2B1=5%2F2
a%2Bb=3%2F2
2.2a%2B2b=3
Add eq. 1 and eq. 2 to eliminate b,
4a-2b%2B2a%2B2b=1%2B3
6a=4
highlight_green%28a=2%2F3%29
Then from eq. 3,
2a%2B2b=3
4%2F3%2B2b=9%2F3
2b=5%2F3
highlight_green%28b=5%2F6%29
.
.
.
y=%282%2F3%29x%5E2%2B%285%2F6%29x%2B1
Complete the square to put the equation into vertex form,y=a%28x-h%29%5E2%2Bk where (h,k) is the vertex.
y=%282%2F3%29x%5E2%2B%285%2F6%29x%2B1
y=%282%2F3%29%28x%5E2%2B%285%2F4%29x%29%2B1
y=%282%2F3%29%28x%5E2%2B%285%2F4%29x%2B25%2F64%29%2B1-%282%2F3%29%2825%2F64%29
y=%282%2F3%29%28x%2B5%2F8%29%5E2%2B96%2F96-25%2F96
y=%282%2F3%29%28x%2B5%2F8%29%5E2%2B71%2F96
.
.
.
Vertex:(-5%2F8,71%2F96)
.
.
.

.
.
.
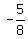The parabola opens upwards.