SOLUTION: How do you solve the following: 32x² + 7x = 81 or 32x² + 7x – 81 = 0 I have tried all possibilities to factor it out with no luck.

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: How do you solve the following: 32x² + 7x = 81 or 32x² + 7x – 81 = 0 I have tried all possibilities to factor it out with no luck.       Log On


   

Question 3349: How do you solve the following: 32x² + 7x = 81 or 32x² + 7x – 81 = 0
I have tried all possibilities to factor it out with no luck.
Answer by drglass(89) About Me  (Show Source):
You can put this solution on YOUR website!
I don't think you will be able to sovle this by factoring. If you are not familiar with the quadratic formula, you probably won't be able to follow my explanation, but, we can find the roots of a quadratic equation (that is, the x values where the equation is 0) using the quadratic formula:

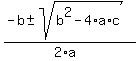
%28-b+%2B-+sqrt%28b%5E2-4%2Aa%2Ac%29%29%2F%282%2Aa%29

For now, let's focus on sqrt%28b%5E2-4%2Aa%2Ac%29

The equation 32x%5E2+%2B+7x+-81 tells us a = 32, b = 7 and c = -81, substituting these values into the formula, we get:

sqrt%287%5E2-4%2A32%2A%28-81%29%29+=+sqrt%2849%2B10368%29+=+sqrt%2810417%29. This is not a perfect square, so factoring won't work, however, continuing with the quadratic formula will.



This gives us a factorization of 32(x - 1.48537)(x + 1.7041)