Question 330626: 1. How many solutions exist for a quadratic equation? Explain and example
2. How do we determine whether the solutions are real or complex? Example.
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! 1.There are always two solutions to a quadratic equation.
They may be a complex conjugate pair solution or a real solution, which includes the possibility of a double root at one x value.
.
.
.
2. Graphically, you can graph the function and see if it ever crosses the x axis. If it does, then the roots are real, if not, then the roots are complex.
Algebraically, use the discriminant,
 where the quadratic equation is in the form  .
If  , two real distinct roots.
If  , one real double root.
If 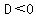 , two complex conjugate pair roots.
.
.
.
.
.
.
The red curve has two real roots,  , 
The green curve has one real double root,  ,
The blue curve has complex conjugate roots,  ,
|
|
|
