Question 23326: 3x - x^2 > 0
Please Help
Found 2 solutions by dkspoet, rapaljer:
Answer by dkspoet(13)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3x-x^2>0
-3x+x^2<0
x(x-3)<0
either x>0 & x-3<0 => x>0 & x<3 => 0 < x < 3
or x<0 & x-3>0 => x<0 & x>3 => can not be true
hence,
0 < x < 3 is the answer
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! I know this problem has already been solved in algebra.com, but I wanted to show how a graphing calculator (or graphing by algebra.com) can be used to solve an inequality.
First graph  , and find the points where the graph crosses or touches the x axis. Draw the graph, and from the previous solution that was posted by another tutor, you should already have the values of x= 0 and x= 3. If you did NOT already have the values of x=0 and x=3, then if you have the graph, then find the x-intercepts. , and find the points where the graph crosses or touches the x axis. Draw the graph, and from the previous solution that was posted by another tutor, you should already have the values of x= 0 and x= 3. If you did NOT already have the values of x=0 and x=3, then if you have the graph, then find the x-intercepts.

The problem says to solve where  , and ">0" means to find all the values of x, where this graph is ABOVE the x-axis. That would be all values of x between 0 and 3. Final answer: , and ">0" means to find all the values of x, where this graph is ABOVE the x-axis. That would be all values of x between 0 and 3. Final answer: 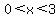 , which in interval notation is (0,3). , which in interval notation is (0,3).
R^2 at SCC
|
|
|