Question 208402: Find an equation for the points (1,1) (2,3) (3,6) and (4, 10).
Found 3 solutions by stanbon, Edwin McCravy, jsmallt9:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an equation for the points (1,1) (2,3) (3,6) and (4, 10).
---------------------------------
I ran a quadratic Regression program on the data and got:
y = (1/2)x^2 +(1/2)x
===============================
Cheers,
Stan H.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Edwin's solution:
Find an equation for the points (1,1) (2,3) (3,6) and (4, 10)
Put down the y values in a row:
1 3 6 10
Find the first successive differences by subtracting
neighboring numbers, and write their differences
between and below them:
1 3 6 10
2 3 4
Find the second successive differences again by
subtracting neighboring numbers, and writing their
differences between and below them:
1 3 6 10
2 3 4
1 1
That took 2 lines of differences until all the differences
were all the same, in this case, 1.
So we know that we need an equation of degree 2.
 Plug in all three points:
Plug in (1,1)
Plug in all three points:
Plug in (1,1)

 Plug in (2,3)
Plug in (2,3)

 Plug in (3,6)
Plug in (3,6)

 You don't need the fourth point.
So you have the system:
You don't need the fourth point.
So you have the system:
 Solve that system and get:
Solve that system and get:
 , ,  and and  Therefore:
Therefore:
 becomes:
becomes:
 or
or
 Factor out
Factor out 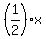 on the right: on the right:
 To take
To take  is the same as dividing by is the same as dividing by  : :
 Edwin
Edwin
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! You listed this problem under "Quadratic Equation" so I assume the problem is to find a quadratic equation for the given points.
The basic form of a quadratic equation is

One way to find the equation is to substitute the coordinates of these points into the basic form. If we take the point (1, 1):

1 = a + b + c
If we use the point (2, 3):

3 = 4a + 2b + c
If we use the point (3, 6):

6 = 9a + 3b + c
At this point we have a system of three equations with three variables (a, b and c). We should be able to solve this for a, b and c. The system is:
1 = a + b + c
3 = 4a + 2b + c
6 = 9a + 3b + c
There are a variety of ways to solve this system: Substitution, Linear Combination (aka Elimination), Cramer's Rule (determinants), and a variety of matrix-based methods. I will use Linear Combination. To start I will subtract the first equation from each of the other two equations. The result of these two subtractions:
2 = 3a + b
5 = 8a + 2b
Now I have a system of two equations of two variables (since the c's have been eliminated).
Now I will subtract twice the first equation from the second. The result of this subtraction:
1 = 2a
Dividing by two we get:
1/2 = a
Now that we have "a" we can substitute for "a" and find "b" and "c". Substituting for a in the second equation of the second system:
5 = 8(1/2) + 2b
5 = 4 + 2b
1 = 2b
1/2 = b
Now we can go back to the first system to find "c". Substituting in "a" and "b" into the second equation of the first system:
3 = 4(1/2) + 2(1/2) + c
3 = 2 + 1 + c
3 = 3 + c
0 = c
Now that we have "a", "b" and "c" we can write our quadratic equation by substituting these values into the basic form:

Substituting:

or

Not only does this equation work for the three points we used, it also works for the fourth point, (4,10).
|
|
|