I really need some help for this problems because I have been confuse of this problems since the start and now the Examination is coming near and this is going to be added, I really will appreciate some help in this questions:
---find the value of k so that the equation  will have equal roots.
will have equal roots.
Find the discriminant  To have equal roots the discriminant must equal 0, so
To have equal roots the discriminant must equal 0, so



 To check, we substitute
To check, we substitute 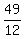 for
for  in
in

 Multiply through by 12 to clear of fractions:
Multiply through by 12 to clear of fractions:



 ;
; 
 ;
; 
 ;
;  So the roots are equal.
-----------------------------------
So the roots are equal.
-----------------------------------
---find the value of k so that the equation  will have one roots numerically equal but opposite in sign
will have one roots numerically equal but opposite in sign
Then it will have to be true that we also get zero when we
substitute  for
for  :
:

 And since we started with
And since we started with  We can set the left sides equal:
We can set the left sides equal:


 Divide thru by 2
Divide thru by 2
 Factor out x
Factor out x

 ;
; 
 So the value of k that will cause the
roots to be numerically equal but opposite
in sign.
Check by substituting -5 for k and solve:
So the value of k that will cause the
roots to be numerically equal but opposite
in sign.
Check by substituting -5 for k and solve:






 and
and  are numerically
equal but opposite in sign.
are numerically
equal but opposite in sign.
--what should be the range of the value of k so that the equation
 will have real and unequal roots.
will have real and unequal roots.
That is when the discriminant is positive
Find the discriminant  "Positive" means the same as "greater than 0"
So we set
"Positive" means the same as "greater than 0"
So we set  Divide through by 9
Divide through by 9
 Since
Since  is never negative the left side will always
positive no matter what value of k we use, so all values of
k will yield real and unequal roots.
So
is never negative the left side will always
positive no matter what value of k we use, so all values of
k will yield real and unequal roots.
So 
---what should be the value of k so that the equation 
will have equal roots?
Find the discriminant  To have equal roots the discriminant must equal 0, so
To have equal roots the discriminant must equal 0, so
 Divide thru by 4
Divide thru by 4




 Using the
Using the  ,
,  Using the
Using the  ,
,  Edwin
Edwin