Question 202413: Solve the formula N=k^2-3k / 2, for k
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Whenever a problem says "Solve for [some variable]" it means "Use Algebra to change the equation around so that the variable is by itself on one side of the equation". So when your problem says "solve for k" it means "change the equation to it looks like k = [....] or [....] = k".
Since k has an exponent of 2 in your equation, solving for k will be a little difficult. I will show two solutions (which will seem different but which, under the covers, are really the same):
Solution 1: Using the Quadratic formula. To use the quadratic formula we need a zero on one side so we will subtract N from both sides giving:

While we could use the quadratic formula now, the fraction will complicate things a little. So we will eliminate the fraction by multiplying both sides of the equation by 2 giving:

The general quadratic equation is:  . The quadratic formula for this is: . The quadratic formula for this is: 
We will use "k" for "x", 2 for "a", -3 for "b" and -2N for "c":

Simplifying


which is our solution.
Solution 2: If you cannot see how the quadratic formula can be used in the way it was used above, the following arrives at a solution without using the quadratic formula. Instead we will "Complete the square".
Completing the square requires an understanding of the binomial (two-term polynomial) square formula:

This says that if a trinomial (3-term polynomial) has a perfect square at the front and another at the back and if the middle term fits the above pattern, then we can rewrite the trinomial as the square of the appropriate binomial.
When we "complete the square" we will manufacture a trinomial of the proper form. Although it may seem mysterious the what and why as I do this, I hope that by the time I am finished you will understand it all.
Since the left side of your equation already starts with a perfect square, k^2, we can proceed to the next step. We will a) find 1/2 of the coefficient of k; b) square the result of (a); and then c) add the result of (b) to both sides of the equation.
(a) 1/2 of 3/2 is 3/4
(b) 
(c) add 9/16 to each side of your equation:

The right side of of this now matches the pattern of the binomial square formula. To see how, let me rewrite it:

(Take a moment so you can see how this is equal to  . Multiply out the last two parts of it.) . Multiply out the last two parts of it.)
Now if we use "k" for "a" and "-3/4" for "b" try to see the 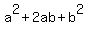 pattern in pattern in  . .
Using the binomial square formula, rewrite the right side:

Before proceeding we will eliminate the fraction on the left by multiplying both sides by 16 giving:

Now we find the square root of both sides. (Remember we need to account for both the positive and negative square roots. This is why we use the +- in front of the square root symbol. The zero in front of the +- is there only because the Algebra.com software won't let me leave it out. The zero is not needed mathematically.)

which simplifies to:

We now have "removed" the exponent of 2 from the "k". We can finish solving for k "normally".
Divide both sides by 4

Now add 3/4

Adding the two fractions on the left:

which is equivalent to the answer we got using the quadratic formula.
|
|
|