Question 189656: Distance from a Point to a Line
4.Find the distance from A(-2,-2) to the line joining B(5,2) and C(-1,4), to the nearest hundredth.
Thanks alot!!!!
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Step 1) Find the equation of the line that passes through the points B(5,2) and C(-1,4)
First let's find the slope of the line through the points ) and and )
Note: ) is the first point is the first point ) and and ) is the second point is the second point ) . .
 Start with the slope formula. Start with the slope formula.
 Plug in Plug in  , ,  , ,  , and , and 
 Subtract Subtract  from from  to get to get 
 Subtract Subtract  from from  to get to get 
 Reduce Reduce
So the slope of the line that goes through the points ) and and ) is is 
Now let's use the point slope formula:
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute
 Multiply Multiply
 Add 2 to both sides. Add 2 to both sides.
 Combine like terms. Combine like terms.
 Simplify Simplify
So the equation that goes through the points ) and and ) is is 
--------------------------------------------------------------------------
Step 2) Find the perpendicular slope
Note: if you draw the line and plot the points, you'll find that the shortest distance is along a perpendicular line from the point to the given line.
Take note that the slope of  is is  . Change the sign and flip the fraction to get . Change the sign and flip the fraction to get  or just or just 
So the perpendicular slope is 
--------------------------------------------------------------------------
Step 3) Find the equation of the line that has a slope of  (the perpendicular slope) and goes through the given point A(-2,-2) (the perpendicular slope) and goes through the given point A(-2,-2)
If you want to find the equation of line with a given a slope of  which goes through the point (-2,-2) you can simply use the point-slope formula to find the equation: which goes through the point (-2,-2) you can simply use the point-slope formula to find the equation:
---Point-Slope Formula---
 where where  is the slope, and is the slope, and ) is the given point is the given point
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite 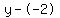 as as 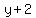
 Rewrite Rewrite 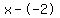 as as 
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 
 Subtract 2 from both sides to isolate y Subtract 2 from both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
So the equation of the line that has a slope of  goes through (-2,-2) is goes through (-2,-2) is 
--------------------------------------------------------------------------
Step 4) Find the point of intersection between the two lines  and and 
 Start with the second equation. Start with the second equation.
 Plug in Plug in 
 Multiply EVERY term by the LCD 3 to clear out the fractions. Multiply EVERY term by the LCD 3 to clear out the fractions.
 Subtract Subtract  from both sides. from both sides.
 Subtract Subtract  from both sides. from both sides.
 Combine like terms on the left side. Combine like terms on the left side.
 Combine like terms on the right side. Combine like terms on the right side.
 Divide both sides by Divide both sides by  to isolate to isolate  . .
 Reduce. Reduce.
 Go back to the second equation. Go back to the second equation.
 Plug in Plug in 
 Multiply Multiply
 Combine like terms. Combine like terms.
So the lines intersect at the point )
--------------------------------------------------------------------------
Step 5) Find the distance between the two points (-2,-2) and )
 Start with the distance formula. Start with the distance formula.
 Plug in Plug in  , ,  , ,  , and , and  . .
 Subtract Subtract 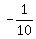 from from  to get to get  . .
 Subtract Subtract  from from  to get to get  . .
 Square Square  to get to get  . .
 Square Square  to get to get  . .
 Add Add  to to  to get to get  . .
 Approximate the right side with a calculator Approximate the right side with a calculator
So the distance between the two points is about 6.008 units.
Rounding this value to the nearest hundredth gives us 
====================================================================
Answer:
So the distance from the point A(-2,-2) to the line joining B(5,2) and C(-1.4) is approximately 6.01 units
Note: if you want more practice, check out this solver
|
|
|