Question 149605: Please help.
1. If x = 1 and x = -8, then form a quadratic equation. I have no idea where to even begin an equation.
2. What type of solution do you get for quadratic equations where D < 0? Give reasons for your answer. Also provide an example of such a quadratic equation and find the solution of the equation.
Iknow if discriminant is less than zero no solutions are defined. But I don't know how to explain why or how to begin an example. Please explain and keep it as simplistic as possible so that I can understand. Like if you were explaining it to a 9 year old.
Thank you so much for all your time and help!!!!!
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
Start with the given zeros
 and and 
Get all terms to the left side in each case (ie subtract 1 from both sides in the first equation and add 8 to both sides in the second equation)
 and and 
Now use the zero product property in reverse to join the factors.

FOIL and multiply

-------------------------------------------
Answer:
So the polynomial with zeros of  and and  is is

Notice how if we graph  , we can see that the polynomial has roots of , we can see that the polynomial has roots of  and and 
 Graph of Graph of  with roots of with roots of  and and 
# 2
Remember the quadratic formula is 
Where the discriminant is  . So the quadratic formula could also look like . So the quadratic formula could also look like 
If D<0, then we'll be taking the square root of a negative number (which we cannot do). So this results in 2 complex solutions (ie no real solutions).
For example, let's find the discriminant for 
From 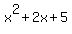 we can see that we can see that  , ,  , and , and 
 Start with the discriminant formula Start with the discriminant formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get 
 Multiply Multiply 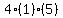 to get to get 
 Subtract Subtract  from from  to get to get 
Since the discriminant is less than zero, this means that there are two complex solutions (or no real solutions)
Now let's use the quadratic formula to find the solutions of 
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 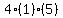 to get to get 
 Subtract Subtract  from from  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of  to get to get 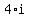 . .
 or or  Break up the expression. Break up the expression.
 or or  Break up the fraction for each case. Break up the fraction for each case.
 or or  Reduce. Reduce.
So our answers are  or or 
Since our answers are complex (non real), this verifies our original claim.
|
|
|