Question 137593This question is from textbook Introductory and Intermediate Algebra
: Problem: Solve polynomial inequality and graph the solution set on a real number line.
(x+1)(x+2)(x+3)>=0
I have set each of the terms to equal 0.
x+1=0 x+2=0 x+3=0
x=-1 x=-2 x=-3
Then I placed these three numbers on a number line as boundary points.
I used the following test points:
-1.5 which was >=0 (true)
-2.5 which was not >=0 (false)
-4 which was not >=0 (false)
0 which was >=0 (true)
I am confused on how to plot this on the number line and write the solution set in set builder notation. I think that I would use [ at -1 and go right, but I am not clear on whether the next point would be set at -2 or -3.
I would have [-1, infinity) and ?
{xIx>=-1 and ?}
Can you help me finish solving this problem. Thank you.
This question is from textbook Introductory and Intermediate Algebra
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your process is right on, but your arithmetic is faulty when you do the tests:

 , (minus times plus times plus is minus), so , (minus times plus times plus is minus), so  produces a false result. produces a false result.
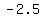 produces a true result (minus times minus times plus is plus) produces a true result (minus times minus times plus is plus)
 produces a false result (minus times minus times minus is minus) produces a false result (minus times minus times minus is minus)
 produces a true result -- this one you got right. produces a true result -- this one you got right.
So, anything smaller than  is false, is false,
Anything between  and and  is true, including is true, including  and and  because of the 'or equal to' part of the original inequality. because of the 'or equal to' part of the original inequality.
Anything between  and and  is false, is false,
And finally, anything larger than or equal to  is true. is true.
Hence your interval is [ , , ] U [ ] U [ , , ) )
The big 'U' stands for 'union' or the set of all elements that are in either or both sets.
A graphical illustration of the situation can be found by multiplying the the three binomials together to get the cubic polynomial 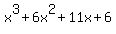 and graph and graph  . The ordered pairs corresponding to those parts of the graph that are either on (equal to) or above (greater than) the x-axis are the solution set of the original inequality. . The ordered pairs corresponding to those parts of the graph that are either on (equal to) or above (greater than) the x-axis are the solution set of the original inequality.

|
|
|