Question 133089: Find the vertex and intercepts for h(x)= -x^2-2x+8 and sketch the graph?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Vertex:
To find the vertex, we first need to find the axis of symmetry (ie the x-coordinate of the vertex)
To find the axis of symmetry, use this formula:

From the equation  we can see that a=-1 and b=-2 we can see that a=-1 and b=-2
 Plug in b=-2 and a=-1 Plug in b=-2 and a=-1
 Negate -2 to get 2 Negate -2 to get 2
 Multiply 2 and -1 to get -2 Multiply 2 and -1 to get -2
 Reduce Reduce
So the axis of symmetry is 
So the x-coordinate of the vertex is  . Lets plug this into the equation to find the y-coordinate of the vertex. . Lets plug this into the equation to find the y-coordinate of the vertex.
Lets evaluate 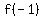
 Start with the given polynomial Start with the given polynomial
 Plug in Plug in 
 Raise -1 to the second power to get 1 Raise -1 to the second power to get 1
 Multiply 2 by -1 to get -2 Multiply 2 by -1 to get -2
 Negate any negatives Negate any negatives
 Now combine like terms Now combine like terms
So the vertex is (-1,9)
Intercepts:
Y-intercept:
To find the y-intercept, simply plug in x=0 and simplify
 Start with the given function Start with the given function
 Plug in Plug in 
 Raise 0 to the 2nd power to get 0 Raise 0 to the 2nd power to get 0
 Multiply -1 and 0 to get 0 Multiply -1 and 0 to get 0
 Multiply 2 and 0 to get 0 Multiply 2 and 0 to get 0
 Subtract 0 from 0 to get 0 Subtract 0 from 0 to get 0
 Add 0 and 8 to get 8 Add 0 and 8 to get 8
So when  , we have , we have  which means that the y-intercept is (0,8) which means that the y-intercept is (0,8)
X-intercept:
To find the x-intercept, plug in y=0 and solve for x
 Start with the given equation Start with the given equation
 Factor the left side (note: if you need help with factoring, check out this solver) Factor the left side (note: if you need help with factoring, check out this solver)
Now set each factor equal to zero:
 or or 
 or or  Now solve for x in each case Now solve for x in each case
So our answer is
 or or 
which means that the x-intercepts are
(-4,0) and (2,0)
--------------------------------------------
Notice if we graph  , we can visually verify our answer , we can visually verify our answer

|
|
|