Question 121328: A quadratic function has x-intercepts at (-8,0) and (2,0). What is the transformational form of the function if the minimum y value is -3?
a) y=3/25(x+3)^2-3
b) 25/3(y+3)=(x+3)^2
c) 25/3(y-3)=(x-3)^2
d) 3/25(y-3)=(x-3)^2
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! A quadratic function has x-intercepts at (-8,0) and (2,0).
What is the transformational form of the function if the
minimum y value is -3?
a) y=3/25(x+3)^2-3
b) 25/3(y+3)=(x+3)^2
c) 25/3(y-3)=(x-3)^2
d) 3/25(y-3)=(x-3)^2
Since it has intercepts (-8,0) and (2,0), the axis of
symmetry must pass through their midpoint, which is
(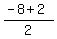 , ,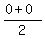 ) or ( ) or (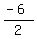 , ,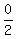 ) = (-3,0)
The axis of symmetry has equation x = h, which is x = -3
The vertex then must be (h,k) where h = -3 and k is the
minimum y value, which is -3.
The equation of a parabola is
c(y-k) = (x-h)^2
c(y-(-3)) = (x-(-3))^2
c(y+3) = (x+3)^2
Since the parabola passes through (2,0)
c(0+3) = (2+3)^2
3c = 5^2
3c = 25
c = 25/3
So
c(y+3) = (x+3)^2
is now ) = (-3,0)
The axis of symmetry has equation x = h, which is x = -3
The vertex then must be (h,k) where h = -3 and k is the
minimum y value, which is -3.
The equation of a parabola is
c(y-k) = (x-h)^2
c(y-(-3)) = (x-(-3))^2
c(y+3) = (x+3)^2
Since the parabola passes through (2,0)
c(0+3) = (2+3)^2
3c = 5^2
3c = 25
c = 25/3
So
c(y+3) = (x+3)^2
is now
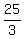 (y+3) = (x+3)^2
So the answer is (b)
Edwin (y+3) = (x+3)^2
So the answer is (b)
Edwin
|
|
|