.
Let a and b be the roots of the quadratic x^2 - 5x + 3 = 0.
Find the quadratic whose roots are a^2/b and b^2/a.
x^2 + ___ x + ___
~~~~~~~~~~~~~~~~~~~~~~~~~
According to Vieta's theorem, we have
a + b = 5,
ab = 3.
Next,  +
+ 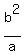 =
=  .
In the numerator,
a^3 + b^3 = (a+b)*(a^2-ab+b^2) = (a+b)*((a^2 +2ab+b^2)-3ab) = (a+b)*((a+b^2-3ab) = (a+b)^3 - 3ab*(a+b) =
substitute here a+b = 5, ab = 3 and continue
= 5^3 - 3*3*5 = 125-45 = 80.
Therefore,
.
In the numerator,
a^3 + b^3 = (a+b)*(a^2-ab+b^2) = (a+b)*((a^2 +2ab+b^2)-3ab) = (a+b)*((a+b^2-3ab) = (a+b)^3 - 3ab*(a+b) =
substitute here a+b = 5, ab = 3 and continue
= 5^3 - 3*3*5 = 125-45 = 80.
Therefore,
 +
+ 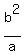 =
=  =
=  .
Also,
.
Also,  .
.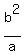 =
=  = ab = 3.
So, due to Vieta's theorem (again), the desired quadratic equation has
the coefficient
= ab = 3.
So, due to Vieta's theorem (again), the desired quadratic equation has
the coefficient  at x and the constant term 3.
ANSWER. The desired quadratic equation is x^2 -
at x and the constant term 3.
ANSWER. The desired quadratic equation is x^2 -  + 3 = 0.
+ 3 = 0.
Solved.