Question 1206740: A truck with a height of 190 cm enters a tunnel with a parabolic ceiling. The width of the truck is 20 m and the maximun height of the tunnel is 10 m. At what minimal distance from the edge of the ground level can this truck pass through the tunnel?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! a parabolic tunnel and a road make a upside down parabola whose vertex is at the top of the tunnel and middle of the road (let it be origin on the graph)
if the maximum height of the tunnel is 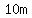 , vertex is at ( , vertex is at ( , , )=( )=( , , ) )
since given that the width of the tunnel is 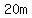 , the edges of the tunnel at road level are , the edges of the tunnel at road level are 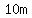 from each side of the middle of road (placed in origin), and we have points from each side of the middle of road (placed in origin), and we have points
( , , ) and ( ) and ( , , ) )
The equation of a parabola will be:
 ...substitute ...substitute  and and 


To find the value of the constant  , use either edge of the points above. , use either edge of the points above.
( , , ) )




so, your equation is

we are looking for the value of when the when the  value is the height of the truck, value is the height of the truck, 






The truck can pass through the tunnel  from the center of the tunnel and from the center of the tunnel and  will be left on each side from the edge. will be left on each side from the edge.
So, minimal distance from the edge of the ground level the truck can pass through the tunnel is  . .

|
|
|