Question 1205723: Solve the system using the substitution method. If there is exactly one solution, write as an ordered pair. If not, choose one of the other options.
{(6x,+,2y,=,34),(x,,,=,-4y+24):}
A. One solution:
B. No solution
C. Infinite number of solutions
Found 3 solutions by ikleyn, josgarithmetic, MathLover1:
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the system using the substitution method. If there is exactly one
solution, write as an ordered pair. If not, choose one of the other options.
6x + 2y = 34
x = -4y + 24
A. One solution:
B. No solution
C. Infinite number of solutions
~~~~~~~~~~~~~~~~~~~~~~~
You are lucky: you are given the system of equations, which is just ready for using the substitution method.
Indeed, the second equation expresses x implicitly via y.
So, substitute this expression of second equation into first equation.
You will get then
6*(-4y+24) + 2y = 34.
Thus, you have now one equation with only one unknown y.
Simplify it and solve for y
-24y + 144 + 2y = 34
-24y + 2y = 34 - 144
-22y = -110
y = 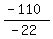 = 5.
Thus you just found out one unknown y: y = 5.
To find x, use the second given equation
x = -4y + 24 = -4*5 + 24 = -20 + 24 = 4.
ANSWER. The problem has one and only one solution x= 4, y= 5.
To check your solution, substitute these found values into equations
and make sure that in each equation the number in the left side is the same as in the right side. = 5.
Thus you just found out one unknown y: y = 5.
To find x, use the second given equation
x = -4y + 24 = -4*5 + 24 = -20 + 24 = 4.
ANSWER. The problem has one and only one solution x= 4, y= 5.
To check your solution, substitute these found values into equations
and make sure that in each equation the number in the left side is the same as in the right side.
Solved, with all necessary explanations.
/////////////////////
From my post, learn how to write your problem, when you post it to this forum.
Do not use so many commas: they are unnecessary, so take them out.
Simply write each equation in separate line and do not use commas.
Also, do not use curved brackets: they also are unnecessary.
Happy learning (!)
Come again to this forum soon to learn something new.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by MathLover1(20849)   (Show Source): (Show Source):
|
|
|