SOLUTION: A certain pawikan breeding site is said to be able to sustain 10000 pawikans. One thousand pawikans are brought there initially. After a year, this increased to 1500 pawikans. Ho

In this problem, the formula for y contains three unknown parameters: "K", "C" and "k".

Fortunately, the three independent conditions are given, that allow to determine all 
three parameters.


First, the limit capacity is given of 10000 pawikans. It means, that in the formula
for "y" we have 

    K = 10000.        (1)

(when t --> oo (infinity), the term    is zero).



Second, for t= 0 (initial condition), we have (substituting t= 0 into the formula for y)

    K - C = 1000      (2)


Via (1), it gives

    C = K - 1000 = 10000 - 1000 = 9000.



Finally, for t= 1, another condition is given ("after a year")

    K -  = 1500    (3).


It gives

     = 1500,

     = 1500 - 10000,

     =    -8500

     = 

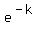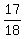     =  =  =  = 0.944444444... = 0.944444444  (approximately).



Now you know all the parameters in the given logistic formula to calculate everything you need.


In paricular, the population of pawikans after 5 years is

    y =  =  = 3237.230574 = 3237  (rounded to the closest integer value).