SOLUTION: Determine the maximum sales and optimal price. a) Bob can sell 200 cars at $20 000 each but finds that every $1000 increase in price causes a 5-car drop in sales Thanks :)

According to the condition, the number of sold cars "n" is THIS function of the price "p" per single car

    n(p) = 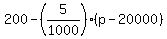 = 200 - 0.005*(p-20000) = -0.005p + 300.     (1)



The revenue ( = the sales) is then the product  R(p) = p*n(p)

    R(p) = p*n(p) = p*(-0.005p + 300) = - 0.005p^2 + 300p.    (2)



Thus the revenue is this quadratic function (2) of the price.



It is well known fact that the general form quadratic function  y = ax^2 + bx + c

with the negative leading coefficient "a" has the maximum at  x = .



In our case,  a= -0.005,  b= 300.  Therefore, the quadratic function (2) has maximal value at  

    q = 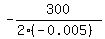 =  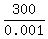= 30000.


So, the optimal price is $30000.



Then the number of the sold cars will be only  n(30000) = -0.005*30000 + 300 = 150,

but the revenue will be  R = 150*30000 = 4,500,000  against  200*20000 = 4,000,000  at the price of $20000.