SOLUTION: The cubic equation x^3-12x^2+ax-48=0 has roots p,2p and 3p. Find the value of p.

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: The cubic equation x^3-12x^2+ax-48=0 has roots p,2p and 3p. Find the value of p.       Log On


   

Question 1099436: The cubic equation x^3-12x^2+ax-48=0 has roots p,2p and 3p. Find the value of p.
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
According to Vieta's theorem, the product of the roots is equal to the constant term taken with the opposite sign in this case.


In the mathematical form,  p*(2p)*(3p) = 48,   or

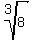6p^3 = 48  ====>  p^3 = 48%2F6 = 8  ====>  p = root%283%2C8%29 = 2.


Answer.  p = 2.


It is INTERESTING that under the given condition, the answer DOES NO DEPEND on the value of the coefficient "a" of the given equation. 


    In opposite, by knowing all the roots p= 2, 2p = 4  and  3p= 6, we can calculate the coefficient "a" 

    (using again the Vieta's theorem) as the sum of all pair-wise products of the roots:


    a = 2*4 + 2*6 + 4*6 = 8 + 12 + 24 = 44.