Question 1099374: Suppose an object is thrown from a platform that is 300 ft. above the Earth with a beginning velocity of +7 ft/sec. How fast is it going at t = 2 seconds?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The acceleration of gravity (anywhere you can stand on Earth) is  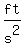 in magnitude (absolute value).
That is the number to use in physics problems.
A beginning velocity of +7 ft/s means nothing,
until we agree on which direction we use for positive distances, velocities, and accelerations.
If the object was thrown up,
a starting velocity of +7 ft/s means 7 ft/s in an upwards direction,
and everything upwards is positive, downwards is negative.
Then, acceleration is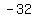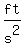 
velocity (in ft/s) as a function of  (time in seconds since the object was released) will be
 until the object hits the ground,
and at  , assuming the object has not hit the ground,
 .
At t=2 seconds, the object is moving downwards, at 57 ft/s .
It obviously has not hit the ground yet, because even going at  for the full 2 seconds, it would not have covered the 300 ft distance.
If the object was thrown down,
a starting velocity of +7 ft/s means 7 ft/s in an downwards direction,
and everything downwards is positive, upwards is negative.
Then, acceleration is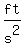
velocity (in ft/s) as a function of (time in seconds since the object was released) will be
 until the object hits the ground,
and at , assuming the object has not hit the ground,
 .
At t=2 seconds, the object is moving downwards, at 61 ft/s .
It obviously has not hit the ground yet, because even going at for the full 2 seconds, it would not have covered the 300 ft distance.
NOTE:
The height of the platform is useful only to figure out when the object will hit the ground.
Height in feet above the ground will be
 , with the  covering the thrown upwards or downwards possibilities,
and the object will hit the ground at  or  ,
also depending on whether it was thrown upwards or downwards.
The apparent downwards acceleration on a falling object will be slightly less on the Equator,
and slightly more on the poles,
but thosee differences are very small,
and the theoretical/calculated difference from starting on or 300 ft above Earth's surface is much, much, much smaller.
|
|
|
