Question 1091157: Please, help me solve this problem : What is the sum of the squares of the roots of (4x^2 - 9)^4 - 10(4x^2 - 9)^2 + 9 = 0.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please, help me solve this problem : What is the sum of the squares of the roots of (4x^2 - 9)^4 - 10(4x^2 - 9)^2 + 9 = 0.
~~~~~~~~~~~~~~~~~~~
This problem is above the average school math.
It is the level of Math circles or local Math olympiads.
So, I will assume that your level corresponds to it.
Therefore, I will give you the general idea only, leaving implementation to you.
Let me start noticing that the polynomial is of degree 8 and has 8 roots that are real or/and complex numbers.
But do not be worried or scared.
First of all, there is NO NEED to solve the given equation and to find the roots explicitly.
Use the Vieta's theorem instead.
The Vietas's theorem says:
1) the sum of all the roots
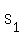 = =  is equal to the coefficient at
is equal to the coefficient at  taken with the opposite sign and divided by the coefficient at taken with the opposite sign and divided by the coefficient at  .
Now notice that the coefficient at .
Now notice that the coefficient at  of the given polynomial is equal to 0 (to zero).
Since I assumed about your level, I will not explain "WHY". It is OBVIOUS.
So, of the given polynomial is equal to 0 (to zero).
Since I assumed about your level, I will not explain "WHY". It is OBVIOUS.
So, 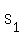 = 0.
2) The sum of all the products of all pairs of the roots = 0.
2) The sum of all the products of all pairs of the roots 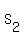 is equal to the coefficient at is equal to the coefficient at 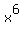 divided by the leading coefficient of the polynomial.
And you need to calculate the coefficient at
divided by the leading coefficient of the polynomial.
And you need to calculate the coefficient at 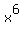 and to find and to find 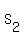 in this way.
Thanks to Vieta, we know now everything that is needed to get the answer.
Indeed, the sum of the squares of the roots in this way.
Thanks to Vieta, we know now everything that is needed to get the answer.
Indeed, the sum of the squares of the roots
 = =  = =  = =  . .
This is the way.
At this point, I just completed my role as a tutor, by providing all the needed instructions to you.
The rest is on you.
|
|
|