Question 1063890: How many complex roots does the equation below have?
x 6 + x 3 + 1 = 0
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Every polynomial of degree "n" has exactly "n" complex roots.
It is the Main Algebra Theorem firstly discovered and proved by famous German mathematician Gauss in 19-th century.
So, the given equation has exactly 6 complex roots in Complex domain.
Regarding your equation
 = 0, (0)
we can solve it explicitly in this way.
First, introduce new variable y = = 0, (0)
we can solve it explicitly in this way.
First, introduce new variable y =  .
In terms of this new equations, the original equation takes the form .
In terms of this new equations, the original equation takes the form
 = 0.
It is a quadratic equation. You can solve it by applying the quadratic formula = 0.
It is a quadratic equation. You can solve it by applying the quadratic formula
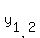 = =  = =  = =  .
So, one root is .
So, one root is  = =  . The other root is . The other root is  = =  .
You can write these complex numbers (complex roots) in a trigonometric (polar) form: .
You can write these complex numbers (complex roots) in a trigonometric (polar) form:
 = =  = = 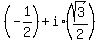 = =  . The modulus is . The modulus is  = =  = = 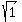 = 1 and the argument is = 1 and the argument is  . .
 = =  = =  = =  . The modulus is . The modulus is  = =  = = 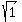 = 1 and the argument is = 1 and the argument is  .
Next, since .
Next, since  = =  , then x = , then x =  = =  .
Now, applying the de Moivre's formula, you have THREE values for x, that all are the cubic roots of the complex number .
Now, applying the de Moivre's formula, you have THREE values for x, that all are the cubic roots of the complex number  : :
 = =  = =  = =  , (1) , (1)
 = =  = =  = =  , (2) , (2)
 = =  = =  = =  . (3)
By the same way as the root . (3)
By the same way as the root  produces the three solutions produces the three solutions  , ,  and and  , the root , the root  produces three other solutions produces three other solutions  , , 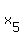 and and 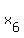 .
Namely, since .
Namely, since  = =  , you have x = , you have x =  = =  .
Now, applying the de Moivre's formula again, you have THREE other values for x, that all are the cubic roots of the complex number .
Now, applying the de Moivre's formula again, you have THREE other values for x, that all are the cubic roots of the complex number  : :
 = =  = =  = =  , (4) , (4)
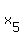 = =  = =  = =  , (5) , (5)
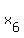 = =  = =  = =  . (6)
These complex numbers, . (6)
These complex numbers,  , ,  , ,  , ,  , , 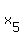 and and 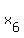 , are all different and are all the roots of the original equation (0).
Probably, this explanation is too complicated for the high school students.
But it is how the university students who study "High Algebra" or/and "Abstract Algebra" solve the equations like (0) in complex domain.
Expressions (1) - (6) could be simplified further and written in rectangular coordinates.
I will not go into these details here.
The complex numbers (1) - (6) lie on the unit circle of the complex domain. , are all different and are all the roots of the original equation (0).
Probably, this explanation is too complicated for the high school students.
But it is how the university students who study "High Algebra" or/and "Abstract Algebra" solve the equations like (0) in complex domain.
Expressions (1) - (6) could be simplified further and written in rectangular coordinates.
I will not go into these details here.
The complex numbers (1) - (6) lie on the unit circle of the complex domain.
There is a bunch of my lessons on complex numbers
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Raising a complex number to an integer power
- How to take a root of a complex number
- Solution of the quadratic equation with real coefficients on complex domain
- How to take a square root of a complex number
- Solution of the quadratic equation with complex coefficients on complex domain
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook.
|
|
|