Question 1050231: Analyze the graph of the quadratic function. (The graph pictured is a parabola, pointing upward with its minimum in quadrant 2, left side mostly in quadrant 4, right side mostly in quadrant 1, and the minimum in quadrant 2 is slightly to the right of the y axis.
The standard form of a quadratic function is f(x) = ax^2 + bx + c. What possible values can a and c have for the given quadratic function Explain your reasoning.
If the vertex from of a quadratic function is f (x) = a(x-h)^2 +k...what possible value can a, h, and k have for the given quadratic function. Epxlain your reasoning.
If the factored form of a quadratic function is f (x) + a(x-r')(x-r")...what possible values can a,r' and r" have? explain your reasoning.
What
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! The description is inconsistent and therefore makes no sense. Look at your graph carefully again and adjust your description. Is the vertex a minimum or a maximum? What quadrant is it in, or if not, on which part of which axis is it? In which quadrants are/is the left branch of the parabola? In which quadrant is/are the right branch of the parabola?
-
Your adjusted description:
The graph pictured is a parabola, pointing upward with its minimum/vertex in quadrant 4, left side mostly in quadrant 2, right side mostly in quadrant 1, and the minimum in quadrant 4 is slightly to the right of the y axis.
The graph will cross the x-axis in two places. One at a negative x value and the other at a positive x value. The minimum being in quadrant 4 means that the k value is negative. The parabola having a MINIMUM for its vertex means that  .
Let me use roots r and s for the roots or x-axis intercepts, and using your factored form,  ----------- this is one of the typical formats for a quadratic function.
Using that form and your parabola as described,
and you can take the r and s variables to help in their meaning as r for RIGHTMOST, and s for SINISTER (meaning to the left or leftmost).
Also according to how you described, the minimum in quadrant 4 is slightly to the right of the y axis, indicates that  . That along with  (but do not becomes confused about order and size).
You can understand this parabola and the values according to the standard form  .
The vertex would be (h,k), and here,  and  .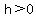
You already know that .
|
|
|
