Question 1048919: For the parabola whose equation is given, determine whether it opens upward or downward, find the vertex, and find the x- and y-intercepts. Then graph the parabola.
f(x)=x squared minus 2 x minus 48
Found 3 solutions by stanbon, MathLover1, advanced_Learner:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! For the parabola whose equation is given, determine whether it opens upward or downward, find the vertex, and find the x- and y-intercepts. Then graph the parabola.
f(x)=x squared minus 2 x minus 48
---
f(x) = x^2 - 2x - 48
a = 1 ; b = -2 ; c = -48
-----
opens upward because a is positive
-------
Vertex::
x = -b/(2a) = 2/2 = 1 ; f(1) = 1^2-2*1-48 = -49
Vertex is (1,-49)
-------------------
x-intercept::
Let y = 0 ; solve for "x"::
x^2-2x-48 = 0
(x-8)(x+6) = 0
x-intercepts:: x = 8 ; x = -6
---------------------------
y-intercept::
Let x = 0 ; solve for "y"::
y = 0^2 - 2*0 - 48
y = -48
----------------
Graph::

------------
Cheers,
Stan H.
-------------
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by advanced_Learner(501)   (Show Source): (Show Source):
You can put this solution on YOUR website! given function
 = =
find
a.opens upward or downward?
b.vertex
c.x intercepts?
d.y-intercepts.
e.graph
Solution

 = =
a= ,b= ,b= ,c= ,c=
therefore,it opens upward since a= is positive. is positive.
 . .
 = =
vertex x part =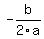
vertex=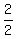
vertex=
vertex y part =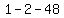
vertex y part=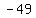
another solution by completing the square.
 = =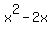
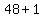 = =
 = =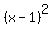 - -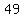 so now the function is written as vertex form so now the function is written as vertex form
 = = 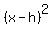 + +
so clearly
 = =
 = =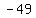
 .x intercepts .x intercepts
 = =
set y= and solve for x and solve for x
 = =
 = =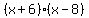
 = = or or  = =
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=196 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 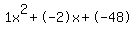 can be factored: can be factored:

Again, the answer is: 8, -6.
Here's your graph:
 |
 .y intercepts .y intercepts
set x= and solve for and solve for 
 = =
 = =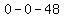
 = =
 .graph .graph
 = =
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=196 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 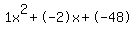 can be factored: can be factored:

Again, the answer is: 8, -6.
Here's your graph:
 |
|
|
|