|
This Lesson (DERIVATION OF LAW OF SINES AND COSINES) was created by by Theo(13342)
  About Theo:
For those of you who are interested, the derivation of the law of sines and the law of cosines is reviewed here.
REFERENCES http://www.regentsprep.org/Regents/math/algtrig/ATT12/derivelawofsines.htm http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofcosines.htm http://www.clarku.edu/~djoyce/trig/laws.html DERIVATION OF LAW OF SINES The main idea is to take a triangle that is not a right triangle and drop a perpendicular from one of the vertices to the opposite side. This splits the triangle into 2 right triangles. You then solve for h in both triangles. h is the altitude of your original triangle. h is also the common leg to both of the right triangles formed. You then use that relationships to derive the law. The attached picture will be used to show how the derivation works. 
The original triangle is ABC which creates right triangles ABD and CBD after dropping a perpendicular from angle B to intersect with AC at D. sine of A is equal to h/c sine of C is equal to h/a Solve for h in both equations to get: h = c * sine of A h = a * sine of C Since both expressions are equal to h, then you can set both expressions equal to each other to get: c * sine of A = a * sine of C sine of A can be shown as sin(A). sine of C can be shown as sin(C). The formula becomes: c*sin(A) = a*sin(C) Divide both sides of this equation by sin(A) and divide both sides of this equation by sin(C) to get: a/sin(A) = c/sin(C) Using the same procedure applied to other angles of the triangle, you can derive the ratios of: a/sin(A) = b/sin(B) and: b/sin(B) = c/sin(C) This leads to the full law of sines which reads: a/sin(A) = b/sin(C) = c/sin(C) For applications involving the law of sines, please see the lesson: http://www.algebra.com/algebra/homework/Trigonometry-basics/THEO-20100406.lesson DERIVATION OF LAW OF COSINES The main idea is to take a triangle that is not a right triangle and drop a perpendicular from one of the vertices to the opposite side. This splits the triangle into 2 right triangles. You then solve for sine of A and Cosine of A in the triangle on the left. You then derive the law of cosines, using the Pythagorean law of right triangles, in the triangle on the right. The relationship between what you solved for in the left triangle and the right triangle establishes the law. The attached picture will be used to show how the derivation works. 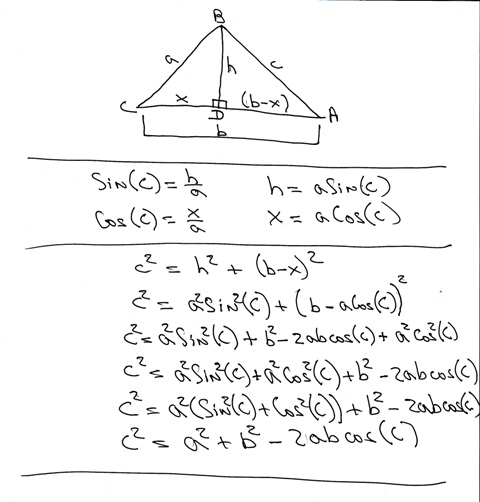
The original triangle is ABC which creates right triangles ABD and CBD after dropping a perpendicular from angle B to intersect with AC at D. We drop a perpendicular from angle B to D on AC. This forms right triangles CBD and ABD. The base of triangle ABC is called side b which we break up into 2 segments called CD and AD. CD is the base of triangle CBD and AD is the base of triangle ABD. The sides of our triangles are labeled as follows: a = side BC which is the hypotenuse of triangle CBD c = side AB which is the hypotenuse of triangle ABD h = side BD which is the altitude of triangle ABC which is also the common leg of right triangle CBD and right triangle ABD. x = side CD which is the other leg of triangle CBD (b-x) = side AD which is the other leg of triangle ABD We use the left triangle (CBD) to form relationships for the sine of angle C and the cosine of angle C. we use the right triangle (ABD) to form relationships from the Pythagorean Theorem. From the left triangle (CBD), we derive: Sine of angle A = opposite / hypotenuse = h/a Cosine of angle A = adjacent / hypotenuse = x/a From these formulas, we derive the following relationships: h = a * Sine of angle A. x = a * Cosine of angle A. Moving to the right triangle (ABD), we derive the following relationships using the Pythagorean Theorem regarding right triangles. That theorem states: The hypotenuse squared of a right triangle is equal to the sum of the other 2 legs of that triangle squared. For the right triangle ABD in our diagram, this relationship becomes: c^2 = h^2 + (b-x)^2 From the left triangle CBD in our diagram, we know that: h = a * sine of C x = a * cosine of C We substitute in the Pythagorean theorem for the right triangle ABD to get: c^2 = (a * sine of C)^2 + (b - a * cosine of C)^2 We use the properties of algebraic operations to simplify this equation. The properties we are using are: (e*f)^2 = e^2*f^2 and: (e-f*g)^2 = e^2 - 2*e*f*g + f^2*g^2) The equation of: c^2 = (a * sine of C)^2 + (b - a * cosine of C)^2 becomes: c^2 = a^2 * (sine of C)^2 + (b^2 - 2 * a * b * cosine of C + a^2 * (cosine of C)^2 sine of C can be shown as sin(C) (sine of C)^2 can be shown as sin^2(C) cosine of C can be shown as cos(C) (cosine of C)^2 can be shown as cos^2(C) our formula becomes: c^2 = a^2 * sin^2(C) + b^2 - 2 * a * b * cos(C) + a^2 * cos^2(C) We can move terms within the equation around without changing the relationship established by the equation to get: c^2 = a^2 * sin^2(C) + a^2 * cos^2(C) + b^2 - 2 * a * b * cos(C) Using the distributive property of algebraic arithmetic of: (e*f + e*g) = e*(f+g), we rearrange our equation to show as: c^2 = a^2 * (sin^2(C) + cos^2(C)) + b^2 - 2 * a * b * cos(C) Another Pythagorean Theorem states that: sin^2(C) + cos^2(C) = 1 This makes our equation become: c^2 = a^2 * (1) + b^2 - 2 * a * b * cos(C) Since a^2 * (1) equals a^2, we simplify this equation to get: c^2 = a^2 + b^2 - 2 * a * b * cos(C) This can also be shown as: c^2 = a^2 + b^2 - 2ab*cos(C) That's one form of the law of cosines. The other forms are: a^2 = b^2 + c^2 - 2bc*cos(A) b^2 = a^2 + c^2 - 2ac*cos(B) For applications involving the law of cosines, please see the lesson: http://www.algebra.com/algebra/homework/Trigonometry-basics/THEO-20100416.lesson This lesson has been accessed 29730 times. |