|
This Lesson (LAW OF SINES) was created by by Theo(13342)
  About Theo:
This lesson provides a review of the Law of Sines and how it is used.
REFERENCES http://www.themathpage.com/aTrig/law-of-sines.htm http://www.clarku.edu/~djoyce/trig/laws.html http://hyperphysics.phy-astr.gsu.edu/hbase/lsin.html http://www.regentsprep.org/Regents/math/algtrig/ATT12/lawofsines.htm http://en.wikipedia.org/wiki/Law_of_sines http://www.univie.ac.at/future.media/moe/galerie/trig/trig.html http://www.regentsprep.org/Regents/math/algtrig/ATT12/lawofsinesAmbiguous.htm The law of sines states that: This means that: This also means that, once you find the common ratio (called R), that: R = R = All of this means that the ratio between the side opposite an angle and the sine of the angle is the same for all sides and angles of that triangle. This law applies to all triangles, not just right triangles. With this law, you can find the measure of all sides of a triangle and all angles of a triangle as long as you are given some basic information. That basic information can include: 2 angles and 1 side. 2 sides and 1 angle opposite one of the given sides. Some examples will show you how this is done. EXAMPLE 1 You are given that 2 sides of a triangle are equal to 3 units and 4 units in length, and the angle opposite the side with 3 units is equal to 36.86989765 degrees. Find the third side and the two other angles of the triangle. First thing you do is draw a triangle and label the angles and the sides. This triangle will be labeled ABC with sides, opposite each corresponding angle, of a,b,c. This means that the side opposite angle A is side a, the side opposite angle B is side b, and the side opposite angle C is side c. A picture of your preliminary triangle is shown below.  We choose one of the angles to be the known angle. We call it angle A. Side a is opposite angle A and is therefore assigned a length of 3 units. We assign side b the length of 4 units. Side c is assigned a length of c. We use its name for its measure until we can find what it's measure is. Angles B and C are assigned their name for their measure as well, for the same reason. We have so far: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = B c = c and angle C = C R = R R is the common ratio that we are looking for. Since we know 1 angle and its opposite side, we can establish what the ratio should be for each of the other angles and their corresponding sides. We set R = The common ratio is equal to 5. We know the length of one other side of this triangle. That side is b and its length is 4. Since the common ratio applies to each of the sides of the triangle divided by the sine of their respective angles, then we can use that ratio to find angle B. Our equation is R = We substitute 5 for R and 4 for b to get: 5 = We divide both sides of this equation by 5 and multiply both sides of this equation by sin(B) to get: sin(B) = We take the arcsine of .8 to get B = 53.13010235 degrees. We now have: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = 53.13010235 degrees c = c and angle C = C R = 5 Since we know that the sum of the angles of any triangle is equal to 180 degrees, we can immediately find angle C by subtracting the sum of angle A and angle B from 180 degrees. We get: Angle C = 180 - 36.86989765 - 53.13010235 = 90 degrees. We have the final angle of the triangle and we can solve for its corresponding side by using the common ratio of 5 one more time to get: 5 = We multiply both sides of this equation by sin(C) to get: Since sin(90) = 1, this equation becomes: 5 = c which is the same as c = 5. We have solved for all sides and all angles of our triangle. They are: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = 53.13010235 degrees c = 5 and angle C = 90 degrees R = 5 To confirm, we take the ratios of each of these to make sure they are all the same. We get: R = R = R = All the ratios are the same so the sides and angles of this triangle have been calculated successfully. A picture of our final triangle is shown below:" 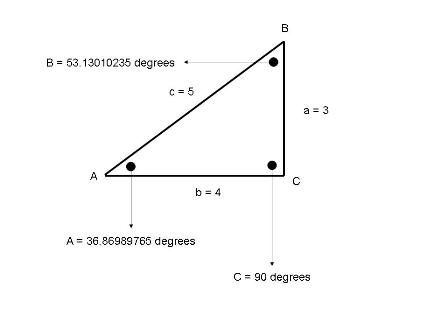 EXAMPLE 2 You are given that 2 angles of a triangle are equal to 13 degrees and 36 degrees, and the side opposite the third angle is equal to 10 units. Find the third angle and the two other sides of the triangle. Since you are given 2 angles of the triangle, you can immediately find the third angle of the triangle because the sum of all three angles of the triangle must equal 180 degrees. Since the sum of the first 2 angles is 13 + 36 = 49 degrees, the third angle must be 131 degrees. Next thing you do is draw a triangle and label the angles and the sides. This triangle will be labeled ABC with sides opposite each corresponding angle of a,b,c. This means that the side opposite angle A is side a, the side opposite angle B is side b, and the side opposite angle C is side c. We choose angle A to be equal to 13 degrees, and angle B to be equal to 36 degrees and angle C to be equal to 131 degrees. Side a will be opposite angle A. Side b will be opposite angle B. Side c will be opposite angle C and will be 10 units in length as given. A picture of your preliminary triangle is shown below: 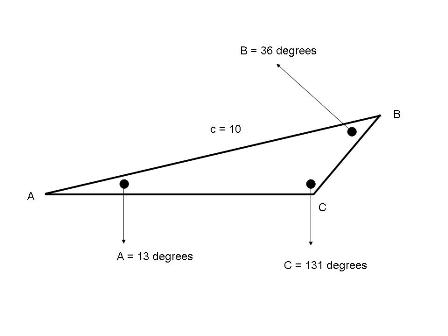 So far we have: a = a and angle A = 13 degrees b = b and angle B = 36 degrees c = 10 and angle C = 131 degrees R = R R is the common ratio we are looking for that applies to all angles and their respective opposite sides. We can find the common ratio by finding out what the ratio of Our equation is: R = Our common ratio is: R = 13.25012993 We use that ratio to get the length of side a using the ratio formula of R = We multiply both sides of this equation by sin(A) to get: a = R * sin(A). We get: a = 13.25012993 * .224951054 = 2.980630694 We use that ratio again to get the length of side b using the ratio formula of R = We multiply both sides of this equation by sin(B) to get: b = R * sin(B). We get: b = 13.25012993 * .587785252 = 7.788230966. We now have all the measures of the triangle. We have: a = 2.980630699 and angle A = 13 degrees b = 7.788230966 and angle B = 36 degrees c = 10 and angle C = 131 degrees R = 13.25012993 To confirm, we take the ratios of each of these to make sure they are all the same. R = R = R = All the ratios are the same so the sides and angles of this triangle have been calculated successfully. A picture of your final triangle is shown below:  THE AMBIGUOUS CASE You might run into a situation where there are two possible solutions to the problem. This is known as the ambiguous case. What makes the ambiguous possible is that the sine of the supplement of an angle is always equal to the sine of the angle. The supplement of an angle is always equal to 180 degrees minus the angle. The following table shows that the sine of the supplement of an angle is always equal to the sine of the angle. The rule works for angles of any size. For example: The angle is 515 degrees and its sine is .422618262. The supplement of the angle is 180 - 515 = -335 degrees and its sine is .422618262. Only positive angles less than or equal to 180 degrees are shown in the table since any interior angle of a triangle has to be greater than 0 degrees and smaller than 180 degrees.
Angle Sine of Angle versus
Angle Sine Supplement Sine Sine of Supplement
30 0.5 150 0.5 Same
60 0.866025404 120 0.866025404 Same
90 1 90 1 Same
100 0.984807753 80 0.984807753 Same
130 0.766044443 50 0.766044443 Same
160 0.342020143 20 0.342020143 Same
THE NO SOLUTION CASE You might also run into a situation where the problem has no solution. This occurs when the Sine of an Angle is greater than 1. This is because the sine of any angle in a triangle can only be from 0 to 1. It also occurs when the sum of 2 angles is greater than or equal to 180 degrees. WHEN TO TEST FOR A NO SOLUTION CASE You always test for the no solution case as part of solving the problem. If you are given 2 angles, then you sum up those angles and, if the sum is greater than or equal to 180 degrees, you have no solution. If you are given 2 sides and 1 angle opposite one of those sides, then you calculate the common ratio from the given angle and its opposite side, and you then calculate the sine of the other angle from its given opposite side. If the sine of that angle is greater than 1, then you have no solution. If the sine of that angle is less than or equal to 1, you calculate the angle. If the sum of that angle and the given angle is greater than or equal to 180 degrees, you have no solution. WHEN TO TEST FOR THE AMBIGUOUS CASE If you are given 2 angles and 1 side, you do not have to test for the ambiguous case because there will not be one. You sum up the 2 given angles and, if the sum is less than 180 degrees, you calculate the third angle. Since all 3 angles are fixed, there is no ambiguity. If you are given 2 sides and 1 angle opposite one of those sides, you will need to test for the ambiguous case. You calculate the common ratio based on the given side and its opposite given angle. You then calculate the sine of the second angle based on the second given side and the common ratio. If the sine of the second angle is greater than 1, then you have no solution. If it is less than or equal to 1, you then calculate the second angle based on its sine. If the sum of the first angle and the second angle is greater than or equal to 180 degrees, then you have no solution. If the sum of the first angle and the second angle is less than 180 degrees, then you have a solution and you can test for the ambiguous case. You test for the ambiguous case by calculating the supplement of the second angle. If the sum of the first angle and the supplement of the second angle is greater than or equal to 180 degrees, then you do not have the ambiguous case. If the sum of the first angle and the supplement of the second angle is less than 180 degrees, then you do have the ambiguous case and there will be 2 solutions to your problem. TESTING FOR THE NO SOLUTION CASE Here's a situation where there is no solution to the problem. EXAMPLE 3 You are given that 2 sides of a triangle are equal to 2 and 4 and that the angle opposite the smaller side is equal to 60 degrees. You are asked to find the third side and the two remaining angles. You create your triangle based on the given information. You label your triangle ABC with respective opposite sides of a,b,c. You assign a = 2 and b = 4 and you assign angle A = 60 degrees. You calculate your common ratio from the given angle and its given opposite side. R = You use R to calculate angle B. Your formula is R = You multiply both sides of this equation by sin(B) and divide both sides of this equation by R to get: sin(B) = You substitute 4 for b and 2.309401077 for R to get: sin(B) = Since the sine of an angle can never be greater than 1, you have no solution to this problem. Here's a situation where there is a valid solution. EXAMPLE 4 You are given that 2 sides of a triangle are equal to 2 and 4 and that the angle opposite the larger side is equal to 60 degrees. You are asked to find the third side and the two remaining angles. You label your triangle ABC with respective opposite sides of a,b,c You assign a = 2 and b = 4 and you assign angle B = 60 degrees. You calculate your common ratio of R = You calculate angle A by using the formula of R = Multiply both sides of this equation by sin(A) and divide both sides of this equation by R to get: sin(A) = You have angle A = 25.65890625 degrees and angle B = 60 degrees. Since the sum of these angles is less than 180 degrees, you have a valid solution and you can now calculate angle C by subtracting the sum of angle A and angle B from 180 degrees. Once you have done that you are on your way to a solution. or possibly 2 solutions, depending on whether you have an ambiguous case or not. TESTING FOR THE AMBIGUOUS CASE You test for the ambiguous case by determining if the sum of the first angle you are given and the supplement of the second angle you have calculated is equal to or greater than 180 degrees. If it is equal to or greater than 180 degrees, then the ambiguous case is not possible and you can only have one solution. If it is less than 180 degrees, then the ambiguous case is possible and you need to find what that second solution is. The following example is taken from example 1 where the ambiguous case exists. We did not test for the ambiguous case when we did example 1 because we were not introduced to the possibility of an ambiguous case until later in this lesson. Now that we know what the ambiguous case is, and now that we know that example 1 needed to be tested for the ambiguous case, we will test for it now. EXAMPLE 5 the problem in example 1 was presented in the following manner: You are given that 2 sides of a triangle are equal to 3 units and 4 units in length, and the angle opposite the side with 3 units is equal to 36.86989765 degrees. Find the third side and the two other angles of the triangle. We assigned side a to be equal to 3 units in length and angle A opposite to side a to be equal to 36.86989765 degrees. We used the common ratio formula of R = We assigned side b to be equal to 4 units in length and angle B opposite to side b to be equal to B degrees. We used that common ratio to find angle B equal to 53.13010235 degrees. Since we were given 2 sides and one angle opposite one of those sides, we needed to test for the ambiguous case. We test by taking the supplement of angle B, that we just calculated, and adding that to angle A, that we were given. The supplement of angle B is equal to 180 - 53.13010235 = 126.8698976 degrees. When added to angle A, that gives us a total of 36.86989765 plus 126.8698976 equals 163.7397953 degrees. Since the sum of angle A plus the supplement of angle B is less than 180 degrees, the ambiguous case exists and a second solution needs to be calculated. We complete the calculation of the first solution, then work on the second solution. The first solution was calculated to be: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = 53.13010235 degrees c = 5 and angle C = 90 degrees R = 5 We proceed to replace angle B with the supplement of angle B and then calculate the remaining sides and angles. We now have: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = 126.8698976 degrees c = c and angle C = C R = 5 We can now calculate angle C to be 180 - angle A - angle B = 16.26020471 degrees. We now calculate c to be equal to 5 * sin(16.26020471) = 1.4. This was based on the common ratio formula of R = Our second possible solution is: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = 126.8698976 degrees c = 1.4 and angle C = 16.26020471 degrees R = 5 To confirm, we take the ratio of all measures to see that they all equal to 5. a/sin(A) = 5 b/sin(B) = 5 c/sin(C) = 5 All measures are good and we have 2 possible solutions to to this problem. The first solution we calculated in example 1. The second solution we calculated in this example 5. The first solution is: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = 53.13010235 degrees c = 5 and angle C = 90 degrees R = 5 The second solution is: a = 3 and angle A = 36.86989765 degrees b = 4 and angle B = 126.8698976 degrees c = 1.4 and angle C = 16.26020471 degrees R = 5 A picture of the first solution for example 1, found in Example 1, and the second solution for example 1, found in Example 5, is shown below:
The following example is taken from example 4 where the ambiguous case is not possible. EXAMPLE 6 The problem in example 4 was presented in the following manner: You are given that 2 sides of a triangle are equal to 2 and 4 and that the angle opposite the larger side is equal to 60 degrees. You are asked to find the third side and the two remaining angles. We did not calculate an original solution for example 4, so we'll do it now. Label your triangle ABC with respective opposite sides of a,b,c. Assign a = 2 and b = 4 and assign angle B = 60 degrees. A picture of your preliminary triangle is shown below:  You have: a = 2 and angle A = A b = 4 and angle B = 60 degrees c = c and angle C = C R = R Compute your common ratio by taking Compute angle A by using the formula R = Multiply both sides of that equation by sin(A) and divide both sides of that equation by R to get: sin(A) = Take the arcsine of .433012702 to get angle A = 25.65890627. You now have: a = 2 and angle A = 25.65890627 degrees b = 4 and angle B = 60 degrees c = c and angle C = C R = 4.618802154 You can now find angle C by taking the sum of 25.65890627 and 60 degrees and subtract that from 180 to get C = 94.34109373 degrees. You use the ratio of R to get R = Multiply both sides of this equation by sin(C) to get: c = sin(C) * R. Substitute known values for R and sin(C) to get: c = 4.605551276 You now have a full solution of: a = 2 and angle A = 25.65890627 degrees b = 4 and angle B = 60 degrees c = 4.605551276 and angle C = 94.34109373 degrees R = 4.618802154 A picture of your final triangle is shown below:  Since you were given 2 sides and 1 angle opposite one of those sides, you need to test for the possibility of a second solution. You were given angle B and you calculated angle A based on the common ratio and the given side a. You take the supplement of angle A and add it to angle B. Supplement of angle A is 180 - 25.65890627 = 154.3410937. When you add 60 degrees of angle B to 154.3410937 degrees, you get a total of 214.3410937 degrees. Since the sum of those 2 angles is greater than 180 degrees, than a second solution is not possible and the solution you have just calculated is the only one available for this problem. Remember, you only have to test for the ambiguous case when you are given 2 sides and 1 angle opposite one of the given sides. HOW TO DETERMINE WHETHER YOU SHOULD USE THE LAW OF SINES OR THE LAW OF COSINES OR THE PYTHAGOREAN FORMULA The law of sines and the law of cosines both solve for the sides and angles of any triangles, including right triangles. The use of one or the other depends on what you are given. If you are given two sides and the included angle, then use the Law of Cosines. If you are given three sides, then use the Law of Cosines. If you are given two sides and an angle opposite one of those sides, then use the Law of Sines. If you are given two angles and one side, then use the Law of Sines. If you know that the triangle you are dealing with is a right triangle, then use the Pythagorean Formula. The lesson on the Law of Cosines can be found by clicking on the following link. LAW OF COSINES The lesson on derivation of law of sines and law of cosines can be found by clicking on the following link: http://www.algebra.com/algebra/homework/Trigonometry-basics/THEO-2012-01-16.lesson This lesson has been accessed 15888 times. |
