SOLUTION: {{{ x^2-2x-3= sqrt( 4 ) }}}. I tried my best to do this but i cant figure this one out can you please help me.

Algebra ->  Test -> SOLUTION: {{{ x^2-2x-3= sqrt( 4 ) }}}. I tried my best to do this but i cant figure this one out can you please help me.      Log On


   

Question 874572: +x%5E2-2x-3=+sqrt%28+4+%29+.
I tried my best to do this but i cant figure this one out can you please help me.
Found 2 solutions by Alan3354, mxgirl22:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
+x%5E2-2x-3=+sqrt%28+4+%29+
+x%5E2-2x-3=+2
+x%5E2-2x-5=+0
---
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-2x%2B-5+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-2%29%5E2-4%2A1%2A-5=24.

Discriminant d=24 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--2%2B-sqrt%28+24+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-2%29%2Bsqrt%28+24+%29%29%2F2%5C1+=+3.44948974278318
x%5B2%5D+=+%28-%28-2%29-sqrt%28+24+%29%29%2F2%5C1+=+-1.44948974278318

Quadratic expression 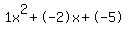1x%5E2%2B-2x%2B-5 can be factored:
1x%5E2%2B-2x%2B-5+=+%28x-3.44948974278318%29%2A%28x--1.44948974278318%29
Again, the answer is: 3.44948974278318, -1.44948974278318. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-2%2Ax%2B-5+%29

============
+x%5E2-2x-3=+-2
+x%5E2-2x-1+=+0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-2x%2B-1+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-2%29%5E2-4%2A1%2A-1=8.

Discriminant d=8 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--2%2B-sqrt%28+8+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-2%29%2Bsqrt%28+8+%29%29%2F2%5C1+=+2.41421356237309
x%5B2%5D+=+%28-%28-2%29-sqrt%28+8+%29%29%2F2%5C1+=+-0.414213562373095

Quadratic expression 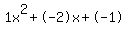1x%5E2%2B-2x%2B-1 can be factored:
1x%5E2%2B-2x%2B-1+=+%28x-2.41421356237309%29%2A%28x--0.414213562373095%29
Again, the answer is: 2.41421356237309, -0.414213562373095. Here's your graph:
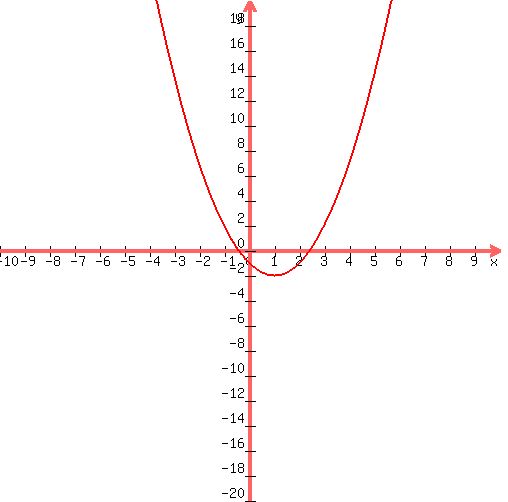graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-2%2Ax%2B-1+%29

=============
Check all the solutions, make sure they're not extraneous.

Answer by mxgirl22(39) About Me  (Show Source):
You can put this solution on YOUR website!
+x%5E2-2x-3=+sqrt%28+4+%29+

x%5E2-2x-3=+2

x%5E2-2x-3-2=2-2

x%5E2-2x-5=0

Now that we have the equation set to zero, we can use the quadratic formula.

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-2x%2B-3+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-2%29%5E2-4%2A1%2A-3=16.

Discriminant d=16 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--2%2B-sqrt%28+16+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-2%29%2Bsqrt%28+16+%29%29%2F2%5C1+=+3
x%5B2%5D+=+%28-%28-2%29-sqrt%28+16+%29%29%2F2%5C1+=+-1

Quadratic expression 1x%5E2%2B-2x%2B-3 can be factored:
1x%5E2%2B-2x%2B-3+=+1%28x-3%29%2A%28x--1%29
Again, the answer is: 3, -1. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-2%2Ax%2B-3+%29