Question 869952: A farmer has 3000 feet of wire to enclose a rectangular field. He plans to fence the entire area and then subdivide it by running a perpendicular fence across the middle. Find the dimensions of the field that would enclose the maximum area . What is the maximum area?
Can you please help me ? Thanks so much in advance I really appreciate it:)
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A farmer has 3000 feet of wire to enclose a rectangular field.
He plans to fence the entire area and then subdivide it by running a perpendicular fence across the middle.
Find the dimensions of the field that would enclose the maximum area .
What is the maximum area?
:
With a fence down the middle we have 2 lengths and 3 widths, therefore:
2L + 3W = 3000
simplify, divide by 2
L + 1.5W = 1500
L = -1.5W + 1500, we can use this form for substitution
:
Area
A = L * W
Replace L with (-1.5W+1500)
A = (-1.5W+1500) * W
A = -1.5W^2 + 15W
From this we can write a quadratic equation, y = A, x=W
y = -1.5W^2 + 1500W
Max area occurs on the axis of symmetry, x=-b/(2a), so we have
x = 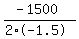
x = 
x = +500 ft is the width for max area
Find L, replace W with 500
L = -1.5(500) + 1500
L = 750 ft is the length for max area
Find the Area
A = 750 * 500
A = 375,000 sq/ft
:
:
You can confirm this your self, find the area using the equation, W=500
A = -1.5W^2 + 1500W
|
|
|