Question 783366: show that maximum area of rectangle ins
cribed in a circle is sqaure
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! DISCLAIMER: I do not know what answer is expected, because it depends on what has been covered in class before, and the rigor and detail expected in the proof. (The fact that it has been 50 years since I last had a geometry class, in 7th grade, does not help). There has to be a simpler, clear, understandable, elegant, rigurous proof, but I could not figure it. The question has been asked and answered before in this website. I just hope at least one of my approaches to a solution is understandable.
USING ALGEBRA:
Let's center a circle with radius  at the origin of x-y coordinates. at the origin of x-y coordinates.
Let's orient the rectangle with sides parallel to the coordinate axes.

Point A (x,y) has positive coordinates, and since it's part of the circle,
 --> --> 
 and and 
the rectangle has


Let me change variables, saying that 
 is a quadratic function with zeros at is a quadratic function with zeros at  and and  . .
The function 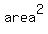 has a maximum, and it is, of course, half-way between the zeros, at has a maximum, and it is, of course, half-way between the zeros, at  . .
That where the maximum area occurs.
That happens when  , ,
which means  , ,
which means  , ,
which means  , ,
which means ABCD is a square.
TRYING TO DO JUST GEOMETRY:
From the point of view of geometry, a square is a rectangle (a special kind of rectangle).
If a rectangle (special or not) is inscribed in a circle, its diagonals are diameters of the circle.
They bisect each other, at the center (O) of the circle.
Each diagonal splits the rectangle into 2 congruent triangles.
We can take the diagonal as the base of the triangles.
We know the length of the base because it is the diameter of the circle.
We can draw the altitude of one of those triangles as a segment of the perpendicular to the base that passes through the other vertex.
I drew the altitude (EB) for triangle ABC in green in the picture below.

The length of altitude EB is the height of the triangles, which depends of the particular rectangle used.
In my drawing, it is shorter than radius OB, which is the hypotenuse of right triangle OEB.
The area of one of the triangles is the base times the height, divided by 2.
The area of the rectangle is the total area of both triangles, and it is the base times the height.
In other words, the area of the rectangle is the diameter of the circle times the height of the triangles.
To get a larger area for the rectangle we need a larger height for the triangles.
The height of those triangles depends on the shape of the rectangle.
If the rectangle is a square, that height is half of the other diagonal, because the diagonals of a square are perpendicular bisectors of each other.
That is the radius of the circle, and the largest possible height.

MIXED APPROACH:
 AC is the diagonal, splitting the rectangle into two congruent right triangles. AC is the diagonal, splitting the rectangle into two congruent right triangles.
AC is also the diameter of the circle.
For right triangle ABC, taking AC is the base, BE is the height.
The area of ABC is 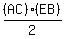 . .
The area of ACD is also 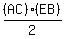 . .
The area of ABCD is the sum, 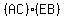 . .
AC is fixed, because it is the diameter of the circle.
BE splits ABC into similar right triangles, and that means
 --> --> 
 and our only variable is and our only variable is 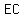 . .
So  . .
 is a quadratic function of is a quadratic function of 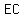 , with a maximum at , with a maximum at  . .
That is the value of EC that maximizes  , making BE maximum, and making , making BE maximum, and making
area of ABCD = 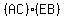 maximum. maximum.
That makes  , so , so  . .
That makes ABE and CBE congruent right triangles, so AB and BC are congruent, and ABCD is a square.
|
|
|