The formula for the perpendicular distance from (x1,y1)
to the line whose equation is Ax+By+C=0 is
d = 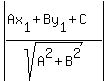 The line has the equation
The line has the equation
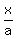 +
+ 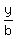 = 1
[Don't get capital A and B confused with little letters a and b]
Clear of fractions by multiplying by LCD = ab:
bx + ay = ab
Get 0 on the right
bx + ay - ab = 0
For (x1,y1) = (0,0)
Substitute in
d =
= 1
[Don't get capital A and B confused with little letters a and b]
Clear of fractions by multiplying by LCD = ab:
bx + ay = ab
Get 0 on the right
bx + ay - ab = 0
For (x1,y1) = (0,0)
Substitute in
d = 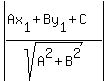 with d = p, A = b, B = a, C = -ab, (x1,y1) = (0,0)
p =
with d = p, A = b, B = a, C = -ab, (x1,y1) = (0,0)
p = 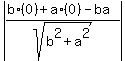 p =
p = 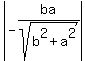 Square both sides
p² =
Square both sides
p² =  Take the reciprocal of both sides:
Take the reciprocal of both sides:
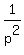 =
= 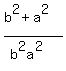 Make two fractions on the right:
Make two fractions on the right:
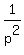 =
= 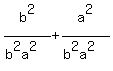
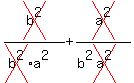
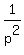 =
= 
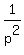 =
= 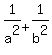 Edwin
Edwin