Question 398582: Find all solutions of the simultaneous equations
2x^2=14+yz
2y^2=14+zx
2z^2=14+xy
I tried everything but i seen to go in a circle I came up to notice that there is pattern meaning that each variable changes position hence it could mean that x=z=y.. but im not sure at all..
help please
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! It is symmetric, but doesn't necessarily mean that x = y = z (we could prove that it's true if it is).
Without loss of generality, suppose  (we can make such an assumption because it's symmetric, but we must also consider negative solutions, if they exist). Then,
 -->  (using substitution)
Taking subsets of the inequality, we get  ,  ,  , which implies  ,  ,  . Since we already have  ,  ,  from our first assumption, this implies  . Setting all variables equal to x, we get  ,  , so ( , , ) is a solution.
If we assume all x,y,z are negative, then by the same logic we get the ordered triple (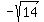 , , 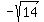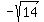) as another solution.
However, what happens if some of the numbers are positive and others are negative? In this case we can assume  . Since the magnitudes of the squares of the numbers are still in order, we get , and the inequalities , , and similar to above. Now, suppose we assume that z is positive. If this is the case, x and y are both positive, and their magnitudes are larger, thus contradiction, so z is negative.
Suppose we subtract the first equation from the second to obtain
 . The left side is positive since the magnitude of y is larger than the magnitude of x. Since z is negative, it follows that x-y is also negative. This implies either:
x is positive, and since y has a magnitude larger than x, y is also positive. However this would not satisfy the inequality (unless x = y).
x is negative, and since y has a larger magnitude and x-y is less than zero, then y is positive. However this would not satisfy in any case (since none of the variables can be zero).
The only possibility is if  and  . If we replace y with x we get the system:
Subtracting the first equation from the second equation,
 Cancel z-x
 -->  -->  . Therefore we can replace y with x, z with x/2 in the first and third equations to obtain:
 --> 
 --> 
These two equations cannot be satisfied, since it implies  (note that x cannot be zero, it can be proven using contradiction that none of x,y,z can equal zero). Therefore there are no solutions in this case.
Thus, the only solutions are when x = y = z, or (, , ) and (, , ).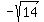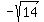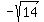
|
|
|
