Question 1210271: If x(x - 3) = - 1, then the value of x³(x³ - 18) will be
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If x(x - 3) = - 1, then the value of x³(x³ - 18) will be
~~~~~~~~~~~~~~~~~~~~~~~~~~
We are given that value of x satisfies equation
x*(x-3) = -1. (1)
In other words, x is the root of the polynomial
p(x) = x^2 - 3x + 1. (2)
They ask to find the value of polynomial Q(x) = x^3*(x^3-18) = x^6 - 18x^3.
To do it, make long division and find the REMAINDER of division Q(x) by p(x)
Q(x) = 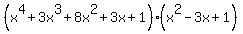 - 1. (3)
Thus, the remainder is -1.
It means, that if you substitute the root x of the polynomial p(x) = x^2 -3x + 1
into polynomial Q(x), then the first addend in the right side of (3) will be 0 (zero),
and you will get the final value of -1 for Q(x).
ANSWER. The value of - 1. (3)
Thus, the remainder is -1.
It means, that if you substitute the root x of the polynomial p(x) = x^2 -3x + 1
into polynomial Q(x), then the first addend in the right side of (3) will be 0 (zero),
and you will get the final value of -1 for Q(x).
ANSWER. The value of 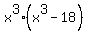 is -1. is -1.
Solved.
---------------------------
The post-solution note
Polynomial p(x) is a quadratic, so it has two roots.
Therefore, you would expect that polynomial Q(x) has two different possible values - but we got only one value, -1.
Why ?
It is because the remainder of division Q(x) by p(x) is not a linear polynomial, as we could expect,
but a single constant value -1, instead.
Therefore, it produces a unique single value -1 for Q(x).
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
|
|
|