.
Find x, 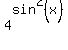 +
+ 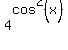 =
= 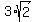 .
.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The original equation is
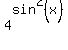 +
+ 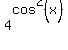 =
= 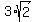 . (1)
Use
. (1)
Use  =
= 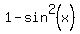 .
Then equation (1) becomes
.
Then equation (1) becomes
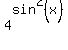 +
+ 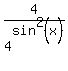 =
= 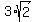 . (2)
Introduce new variable t =
. (2)
Introduce new variable t = 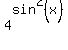 . Then equation (2) takes the form
t +
. Then equation (2) takes the form
t +  =
= 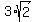 . (3)
Reduce it to the standard form quadratic equation
t^2 + 4 =
. (3)
Reduce it to the standard form quadratic equation
t^2 + 4 =  ,
t^2 -
,
t^2 -  + 4 = 0. (4)
Use the quadratic formula to find the roots
+ 4 = 0. (4)
Use the quadratic formula to find the roots
 =
= 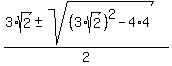 =
= 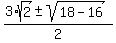 =
=  .
So, equation (4) has two roots.
One root is
.
So, equation (4) has two roots.
One root is  =
= 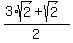 =
=  =
=  .
Another root is
.
Another root is  =
= 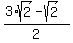 =
= 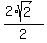 =
=  .
So, further we consider two cases.
Case 1.
.
So, further we consider two cases.
Case 1. 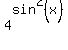 =
=  .
Then
.
Then  =
= 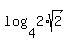 =
= 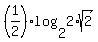 =
= 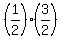 =
=  .
It implies sin(x) = +/-
.
It implies sin(x) = +/-  = +/-
= +/-  .
Hence, x =
.
Hence, x = 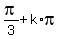 , k = 0, +/-1, +/-2, . . . or x =
, k = 0, +/-1, +/-2, . . . or x = 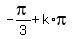 , k = 0, +/-1, +/-2, . . .
Case 2.
, k = 0, +/-1, +/-2, . . .
Case 2. 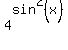 =
=  .
Then
.
Then  =
= 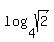 =
= 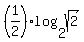 =
= 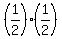 =
=  .
It implies sin(x) = +/-
.
It implies sin(x) = +/-  = +/-
= +/-  .
Hence, x =
.
Hence, x = 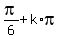 , k = 0, +/-1, +/-2, . . . or x =
, k = 0, +/-1, +/-2, . . . or x = 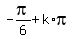 , k = 0, +/-1, +/-2, . . .
ANSWER. The solutions to given equation are these four infinite sets of real numbers
x =
, k = 0, +/-1, +/-2, . . .
ANSWER. The solutions to given equation are these four infinite sets of real numbers
x = 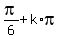 , k = 0, +/-1, +/-2, . . . or x =
, k = 0, +/-1, +/-2, . . . or x = 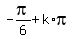 , k = 0, +/-1, +/-2, . . .
or x =
, k = 0, +/-1, +/-2, . . .
or x = 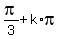 , k = 0, +/-1, +/-2, . . . or x =
, k = 0, +/-1, +/-2, . . . or x = 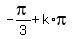 , k = 0, +/-1, +/-2, . . .
, k = 0, +/-1, +/-2, . . .
Solved.