Question 1207271: water runs into a conical tank at the rate of 8 cubic meters per hour. if the height of the cone is 10 meters, and the diameter of its opening is 12 meters, how fast is the water level rising when the water is 3 meters deep?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
water runs into a conical tank at the rate of 8 cubic meters per hour.
if the height of the cone is 10 meters, and the diameter of its opening is 12 meters,
how fast is the water level rising when the water is 3 meters deep?
~~~~~~~~~~~~~~~~~~~
The part of the conical tank, occupied by water, is the cone with the ratio radius to the height
of 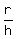 = =  = 0.6.
Hence, the volume of the water in the tank at every time moment t is
V(t) = = 0.6.
Hence, the volume of the water in the tank at every time moment t is
V(t) =  = = 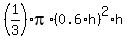 = = 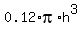 . (1)
Differentiate it by the time . (1)
Differentiate it by the time
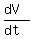 = = 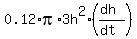 . (2) . (2)
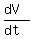 is given: it is the inflow rate, or 8 m^3/hour.
Hence, when h = 3 meters deep, we have from (2)
8 = is given: it is the inflow rate, or 8 m^3/hour.
Hence, when h = 3 meters deep, we have from (2)
8 = 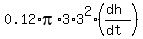 = =  .
Hence, .
Hence, 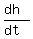 = = 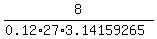 = 0.78595 meters per hour.
Rounding to 3 decimals, you get the
ANSWER. When the water depth is 3 meters, the water rising rate is about 0.786 m/hour. = 0.78595 meters per hour.
Rounding to 3 decimals, you get the
ANSWER. When the water depth is 3 meters, the water rising rate is about 0.786 m/hour.
Solved.
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A drawing of a cross section of the cone, might be helpful for tutor Ikleyn's
solution:
 The part of the conical tank, occupied by water, is the cone with the ratio radius to the height
of
The part of the conical tank, occupied by water, is the cone with the ratio radius to the height
of 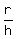 = =  = 0.6.
This is because of corresponding parts of similar right triangles.
Hence, the volume of the water in the tank at every time moment t is
V(t) = = 0.6.
This is because of corresponding parts of similar right triangles.
Hence, the volume of the water in the tank at every time moment t is
V(t) =  = = 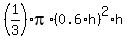 = = 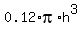 . (1)
The mistake some of my students were prone to make at this point was their
failure to realize that h is a VARIABLE, and not the CONSTANT 3. Some of
my students would try to substitute 3 for h at this point, and didn't
know what to do next. But we must first allow h to vary, and then only
"freeze" the variable at h=3 AFTERWARDS. We must NOT substitute 3 for h
until after we have employed differentiation.
Differentiate it by [with respect to] the time: . (1)
The mistake some of my students were prone to make at this point was their
failure to realize that h is a VARIABLE, and not the CONSTANT 3. Some of
my students would try to substitute 3 for h at this point, and didn't
know what to do next. But we must first allow h to vary, and then only
"freeze" the variable at h=3 AFTERWARDS. We must NOT substitute 3 for h
until after we have employed differentiation.
Differentiate it by [with respect to] the time:
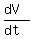 = = 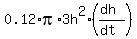 . (2) . (2)
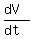 is given: it is the inflow rate, or 8 m^3/hour.
Hence, when h = 3 meters deep, we have from (2)
Notice that she waited until after differentiating the equation for V, to
substitute the "freeze value" of 3 for the variable h. Never substitute the
"freeze value" of a variable too early, but wait until after the calculus has
been applied to substitute it.
8 = is given: it is the inflow rate, or 8 m^3/hour.
Hence, when h = 3 meters deep, we have from (2)
Notice that she waited until after differentiating the equation for V, to
substitute the "freeze value" of 3 for the variable h. Never substitute the
"freeze value" of a variable too early, but wait until after the calculus has
been applied to substitute it.
8 = 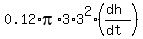 = =  .
Hence, .
Hence, 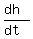 = = 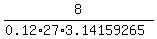 = 0.78595 meters per hour.
Rounding to 3 decimals, you get the
ANSWER. When the water depth is 3 meters, the water rising rate is about 0.786 m/hour.
Notice that the water rising rate of 0.786 m/h occurred only at one instant!
One second before the water became 3 inches deep, the water rising rate was
slightly faster, and then, one second later, the water rising rate was slightly
slower. The water rising rate continued to get slower and slower until the
cone became completely filled. This is because the top of the cone of water
became wider and wider as more water was added. The water rising rate would be
constant when filling a cylinder, but not when filling a cone. = 0.78595 meters per hour.
Rounding to 3 decimals, you get the
ANSWER. When the water depth is 3 meters, the water rising rate is about 0.786 m/hour.
Notice that the water rising rate of 0.786 m/h occurred only at one instant!
One second before the water became 3 inches deep, the water rising rate was
slightly faster, and then, one second later, the water rising rate was slightly
slower. The water rising rate continued to get slower and slower until the
cone became completely filled. This is because the top of the cone of water
became wider and wider as more water was added. The water rising rate would be
constant when filling a cylinder, but not when filling a cone.
|
|
|