SOLUTION: prove that 【(n+1)^n】+1 is divisible by n^2 by using binomial theorem

Algebra ->  Test -> SOLUTION: prove that 【(n+1)^n】+1 is divisible by n^2 by using binomial theorem       Log On


   

Question 1207212: prove that 【(n+1)^n】+1 is divisible by n^2 by using binomial theorem
Answer by Shin123(626) About Me  (Show Source):
You can put this solution on YOUR website!
Unfortunately, that is not true, since taking n=2 gives that 10 is divisible by 4, which is clearly false.
Did you mean 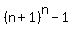%28n%2B1%29%5En-1 instead? In that case, the statement is true, and the proof is as follows.
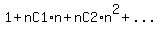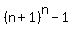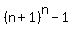To show this, we can expand out %28n%2B1%29%5En with the binomial theorem. Doing so, we get 1%2BnC1%2An%2BnC2%2An%5E2%2B.... Note that all the terms after 1 are divisible by n%5E2 (the second term is just n%5E2), so we have %28n%2B1%29%5En is congruent to 1 mod n%5E2, which means that %28n%2B1%29%5En-1 is congruent to 0 mod n%5E2, aka %28n%2B1%29%5En-1 is divisible by n%5E2.