You can
put this solution on YOUR website! .
The diagonals of a parallelogram are 6cm and 8cm long and they intersect
at an angle of 55°. Calculate the area of the parallogram.
~~~~~~~~~~~~~~~~~
In this parallelogram, the diagonals divide/separate it in 4 (four) triangles.
Two of these 4 triangles are congruent and have the sides 3= 6/2 meters and 4= 8/2 meters
with the concluded angle of 55°.
Two other of these 4 triangles are congruent and have the sides 3= 6/2 meters and 4= 8/2 meters
with the concluded angle of 180° - 55° = 125°.
Therefore, the area of this parallelogram is
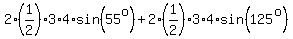= 3*4*0.81915204428 + 3*4*0.81915204428 = 19.65964906 (rounded). ANSWER
Solved.
